A generalized finite element formulation for nonlinear frequency response analysis of viscoelastic sandwich beams using harmonic balance method

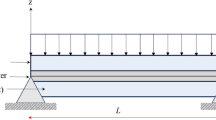
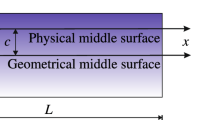
Abstract

Harmonic balance method (HBM) is a popular computational tool for the nonlinear dynamic analysis of structural elements in the frequency domain. Its application in conjunction with the finite element (FE) procedure involves complexity in the formulation of the geometrically nonlinear equation of motion. Further complexity arises in the case of a viscoelastic structure as its constitutive model involves temporal derivative/integral of stress/strain. In this concern, the consideration of a few harmonic terms in HBM poses somewhat simplified formulation, but it may not provide a good theoretical estimation of nonlinear dynamics. Therefore, a large number of harmonic terms in HBM are to be considered despite the corresponding complexity, as well as a high computational cost. In this view, presently, two new formulation strategies are introduced toward a generalized FE formulation, especially for the consideration of an arbitrary number of harmonic terms in HBM. The first strategy lies in the formulation of the geometrically nonlinear stiffness matrix through a special factorization of the nonlinear strain–displacement matrix, while the second one lies in the analytical integration of system matrices/vectors over a time period by exploiting the orthogonality of Fourier basis functions. These formulation strategies provide not only the equation of motion with a reduced number of terms in the HBM-based expanded forms of system matrices/vectors but also a significantly reduced computational time. Additionally, various time–domain viscoelastic constitutive models are reduced into a generalized form for the periodic stress/strain to achieve a common HBM-based FE formulation for any of these viscoelastic material models.

Appendices

Appendix A

For the nine-node plane Lagrange element (Fig. 2), the shape functions are as follows

$$\begin{aligned} N_{1} & = \frac{1}{4}(1 - \xi )(1 - \eta ) - \frac{1}{4}(1 - \xi^{2} )(1 - \eta ) - \frac{1}{4}(1 - \xi )(1 - \eta^{2} ) + \frac{1}{4}(1 - \xi^{2} )(1 - \eta^{2} ) \\ N_{2} & = \frac{1}{4}(1 + \xi )(1 - \eta ) - \frac{1}{4}(1 - \xi^{2} )(1 - \eta ) - \frac{1}{4}(1 + \xi )(1 - \eta^{2} ) + \frac{1}{4}(1 - \xi^{2} )(1 - \eta^{2} ) \\ N_{3} & = \frac{1}{4}(1 + \xi )(1 + \eta ) - \frac{1}{4}(1 + \xi )(1 - \eta^{2} ) - \frac{1}{4}(1 - \xi^{2} )(1 + \eta ) + \frac{1}{4}(1 - \xi^{2} )(1 - \eta^{2} ) \\ N_{4} & = \frac{1}{4}(1 - \xi )(1 + \eta ) - \frac{1}{4}(1 - \xi^{2} )(1 + \eta ) - \frac{1}{4}(1 - \xi )(1 - \eta^{2} ) + \frac{1}{4}(1 - \xi^{2} )(1 - \eta^{2} ) \\ N_{5} & = \frac{1}{2}(1 - \xi^{2} )(1 - \eta ) - \frac{1}{2}(1 - \xi^{2} )(1 - \eta^{2} ) \\ N_{6} & = \frac{1}{2}(1 + \xi)(1 - \eta^{2}) - \frac{1}{2}(1 - \xi^{2} )(1 - \eta^{2} ) \\ N_{7} & = \frac{1}{2}(1 - \xi^{2} )(1 + \eta ) - \frac{1}{2}(1 - \xi^{2} )(1 - \eta^{2} ) \\ N_{8} & = \frac{1}{2}(1 - \xi)(1 - \eta^{2}) - \frac{1}{2}(1 - \xi^{2} )(1 - \eta^{2} ) \\ N_{9} & = \frac{1}{2}(1 - \xi^{2} )(1 - \eta^{2} ) \end{aligned}$$

(A.1)

where $N_{i} \,\,(i = 1,\,\,2,\,\,3,\,.\,.\,.,9)$ is the shape function corresponding to the $i$th node of the finite element.

The linear strain–displacement matrix ${\varvec{B}}_{n}$ appearing in Eq. (26d) can also be written as

$${\varvec{B}}_{n} = {\varvec{B}}_{1}^{L} ({\varvec{I}}_{18 \times 18} \otimes {\varvec{B}}_{1}^{Q} ) + {\varvec{B}}_{2}^{L} ({\varvec{I}}_{18 \times 18} \otimes {\varvec{B}}_{2}^{Q} ) + {\varvec{B}}_{3}^{L} ({\varvec{I}}_{18 \times 18} \otimes {\varvec{B}}_{3}^{Q} ) + {\varvec{B}}_{4}^{L} ({\varvec{I}}_{18 \times 18} \otimes {\varvec{B}}_{4}^{Q} )$$

(A.2)

where the unity matrix (${\varvec{I}}$) appears with the size of $(18 \times 18)$ since there are two degrees of freedom ($u$ and $w$) at every node of the nine-node plane Lagrange element. The other component matrices in Eq. (A.2) appear in the following forms according to the operator matrices in Eq. (26b).

$$\begin{gathered} {\varvec{B}}_{i}^{L} = \left[ {\begin{array}{*{20}c} {{\varvec{B}}_{i}^{L1} } & {{\varvec{B}}_{i}^{L2} } & {{\varvec{B}}_{i}^{L3} } & {{\varvec{B}}_{i}^{L4} } & {{\varvec{B}}_{i}^{L5} } & {{\varvec{B}}_{i}^{L6} } & {{\varvec{B}}_{i}^{L7} } & {{\varvec{B}}_{i}^{L8} } & {{\varvec{B}}_{i}^{L9} } \\ \end{array} } \right],\quad i = 1,2,3,4 \hfill \\ {\varvec{B}}_{i}^{Q} = \left[ {\begin{array}{*{20}c} {{\varvec{B}}_{i}^{Q1} } & {{\varvec{B}}_{i}^{Q2} } & {{\varvec{B}}_{i}^{Q3} } & {{\varvec{B}}_{i}^{Q4} } & {{\varvec{B}}_{i}^{Q5} } & {{\varvec{B}}_{i}^{Q6} } & {{\varvec{B}}_{i}^{Q7} } & {{\varvec{B}}_{i}^{Q8} } & {{\varvec{B}}_{i}^{Q9} } \\ \end{array} } \right],\quad i = 1,2,3,4 \hfill \\ {\varvec{B}}_{1}^{Lq} = \left[ {\begin{array}{*{20}c} {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial x}}} \right. \kern-0pt} {\partial x}}} & 0 \\ 0 & 0 \\ {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial z}}} \right. \kern-0pt} {\partial z}}} & 0 \\ \end{array} } \right],\;{\varvec{B}}_{1}^{Qq} = \left[ {\begin{array}{*{20}c} {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial x}}} \right. \kern-0pt} {\partial x}}} & 0 \\ \end{array} } \right],\;\quad q = 1,2,3.....9 \hfill \\ \,{\varvec{B}}_{2}^{Lq} = \left[ {\,\begin{array}{*{20}c} 0 & 0 \\ {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial z}}} \right. \kern-0pt} {\partial z}}} & 0 \\ {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial x}}} \right. \kern-0pt} {\partial x}}} & 0 \\ \end{array} } \right],{\varvec{B}}_{2}^{Qq} = \left[ {\begin{array}{*{20}c} {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial z}}} \right. \kern-0pt} {\partial z}}} & 0 \\ \end{array} } \right],\quad q = 1,2,3.....9 \hfill \\ \,{\varvec{B}}_{3}^{Lq} = \left[ {\begin{array}{*{20}c} 0 & {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial x}}} \right. \kern-0pt} {\partial x}}} \\ 0 & 0 \\ 0 & {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial z}}} \right. \kern-0pt} {\partial z}}} \\ \end{array} } \right],\;{\varvec{B}}_{3}^{Qq} = \left[ {\begin{array}{*{20}c} 0 & {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial x}}} \right. \kern-0pt} {\partial x}}} \\ \end{array} } \right],\quad q = 1,2,3.....9 \hfill \\ \,{\varvec{B}}_{4}^{Lq} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial z}}} \right. \kern-0pt} {\partial z}}} \\ 0 & {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial x}}} \right. \kern-0pt} {\partial x}}} \\ \end{array} } \right],\;{\varvec{B}}_{4}^{Qq} = \left[ {\begin{array}{*{20}c} 0 & {{{\partial N_{q} } \mathord{\left/ {\vphantom {{\partial N_{q} } {\partial z}}} \right. \kern-0pt} {\partial z}}} \\ \end{array} } \right],\quad q = 1,2,3.....9 \hfill \\ \end{gathered}$$

(A.3)

where $N_{q}$ is the shape function corresponding to the $q^{th}$ node of the finite element, as given in Eq. (A.1).

Appendix B

For a finite number ($H$) of harmonic terms, the Fourier expansion of the nodal displacement vector (${}^{i}{\varvec{d}}_{e}$) can be written as

$${}^{i}{\varvec{d}}_{e} = {}^{i}{\varvec{d}}_{e}^{o} + \sum\limits_{n = 1}^{H} {{}^{i}{\varvec{d}}_{en}^{c} \cos (n\omega t) + {}^{i}{\varvec{d}}_{en}^{s} \sin (n\omega t)}$$

(B.1)

where ${}^{i}{\varvec{d}}_{e}^{o}$, ${}^{i}{\varvec{d}}_{en}^{s}$ and ${}^{i}{\varvec{d}}_{en}^{c}$ are the displacement amplitude vectors for the constant, sine and cosine terms, respectively. Using Eq. (B.1), the Fourier expansion of the term ${}^{i}{\varvec{d}}_{eI}$ (${}^{i}{\varvec{d}}_{eI} = ({\varvec{I}} \otimes {}^{i}{\varvec{d}}_{e} )$) can be written as

$$\begin{gathered} {}^{i}{\varvec{d}}_{eI} = ({}^{i}{\varvec{d}}_{eI} )^{o} + \sum\limits_{q = 1}^{H} {({}^{i}{\varvec{d}}_{eI} )_{q}^{s} \cos (q\omega t) + ({}^{i}{\varvec{d}}_{eI} )_{q}^{c} \sin (q\omega t)} \hfill \\ ({}^{i}{\varvec{d}}_{eI} )^{o} = ({\varvec{I}}_{18 \times 18} \otimes \,{}^{i}{\varvec{d}}_{e}^{o} ),\;({}^{i}{\varvec{d}}_{eI} )_{q}^{s} = ({\varvec{I}}_{18 \times 18} \otimes \,{}^{i}{\varvec{d}}_{eq}^{s} ),\;({}^{i}{\varvec{d}}_{eI} )_{q}^{c} = ({\varvec{I}}_{18 \times 18} \otimes \,{}^{i}{\varvec{d}}_{eq}^{c} ) \hfill \\ \end{gathered}$$

(B.2)

Using Eqs. (B.1) and (B.2), the expanded form of the term $({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )$ can be obtained as

$${}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} = ({}^{i}{\varvec{d}}_{eI} )^{o} \,{}^{i}{\varvec{d}}_{e}^{o} + \left[ \begin{gathered} \sum\limits_{q = 1}^{H} {\left\{ \begin{gathered} \left[ {({}^{i}{\varvec{d}}_{eI} )^{o} \,{}^{i}{\varvec{d}}_{eq}^{c} \, + ({}^{i}{\varvec{d}}_{eI} )_{q}^{c} \,{}^{i}{\varvec{d}}_{e}^{o} } \right]\cos (q\omega t) + \hfill \\ \left[ {({}^{i}{\varvec{d}}_{eI} )^{o} \,{}^{i}{\varvec{d}}_{eq}^{s} \, + ({}^{i}{\varvec{d}}_{eI} )_{q}^{s} \,{}^{i}{\varvec{d}}_{e}^{o} } \right]\sin (q\omega t) \hfill \\ \end{gathered} \right\}} + \hfill \\ \sum\limits_{q = 1}^{H} {\,\sum\limits_{n = 1}^{H} {\frac{1}{2}\left\{ \begin{gathered} \left[ {({}^{i}{\varvec{d}}_{eI} )_{q}^{c} \,{}^{i}{\varvec{d}}_{en}^{c} } \right]\left[ {\cos (q + n)\omega t + \cos (q - n)\omega t} \right] + \hfill \\ \left[ {({}^{i}{\varvec{d}}_{eI} )_{q}^{s} \,{}^{i}{\varvec{d}}_{en}^{s} } \right]\left[ {\cos (q - n)\omega t - \cos (q + n)\omega t} \right] + \hfill \\ \left[ {({}^{i}{\varvec{d}}_{eI} )_{q}^{c} \,{}^{i}{\varvec{d}}_{en}^{s} } \right]\left[ {\sin (q + n)\omega t - \sin (q - n)\omega t} \right] + \hfill \\ \left[ {({}^{i}{\varvec{d}}_{eI} )_{q}^{s} \,{}^{i}{\varvec{d}}_{en}^{c} } \right]\left[ {\sin (q + n)\omega t + \sin (q - n)\omega t} \right] \hfill \\ \end{gathered} \right\}\,} } \hfill \\ \end{gathered} \right]$$

(B.3)

Alternatively, the expanded form of the term $({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )$ can be written following the conventional form of Fourier series as

$${}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} = ({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )^{o} + \sum\limits_{m = 1}^{2H} {({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{c} \cos (m\omega t) + ({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{s} \sin (m\omega t)}$$

(B.4)

where $({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )^{o}$, $({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{c} \,$ and $({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{s} \,$ are the amplitude vectors for the constant, cosine and sine terms, respectively. It is clear from Eqs. (B.3) and (B.4) that any of the amplitude vectors $({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )^{o}$/$({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{c} \,$/$({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{s} \,$ comprises of the coefficient matrices ($({}^{i}{\varvec{d}}_{eI} )^{o}$, $({}^{i}{\varvec{d}}_{eI} )_{q}^{s}$, $({}^{i}{\varvec{d}}_{eI} )_{q}^{c}$) and coefficient vectors (${}^{i}{\varvec{d}}_{e}^{o}$, ${}^{i}{\varvec{d}}_{en}^{s}$, ${}^{i}{\varvec{d}}_{en}^{c}$) in the Fourier expansion of ${}^{i}{\varvec{d}}_{e}$ (Eq. B.1) and ${}^{i}{\varvec{d}}_{eI}$ (Eq. B.2). Therefore, the coefficient matrices $({}^{i}{\varvec{d}}_{eI} )^{o}$, $({}^{i}{\varvec{d}}_{eI} )_{q}^{s}$ and $({}^{i}{\varvec{d}}_{eI} )_{q}^{c} \,$) in an amplitude vector ($({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )^{o}$/$({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{c} \,$/$({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{s} \,$) are taken together within a matrix (${\varvec{D}}^{o}$/${\varvec{D}}_{m}^{c}$/$\,{\varvec{D}}_{m}^{s}$), while the associated coefficient vectors (${}^{i}{\varvec{d}}_{e}^{o}$, ${}^{i}{\varvec{d}}_{en}^{s}$ and ${}^{i}{\varvec{d}}_{en}^{c}$) are taken in the form of a generalized nodal displacement amplitude vector (${}^{i}{\varvec{X}}_{e}$) according to the following expressions

$$\begin{gathered} ({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )^{o} = {\varvec{D}}^{o} {}^{i}{\varvec{X}}_{e} ,\;({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{c} = {\varvec{D}}_{m}^{c} {}^{i}{\varvec{X}}_{e} ,\;\,({}^{i}{\varvec{d}}_{eI} {}^{i}{\varvec{d}}_{e} )_{m}^{s} = {\varvec{D}}_{m}^{s} {}^{i}{\varvec{X}}_{e} \hfill \\ {}^{i}{\varvec{X}}_{e} = \{ \begin{array}{*{20}c} {({}^{i}{\varvec{d}}_{e}^{o} )^{{\text{T}}} } & {({}^{i}{\varvec{d}}_{e1}^{c} )^{{\text{T}}} } & {({}^{i}{\varvec{d}}_{e2}^{c} )^{{\text{T}}} } \\ \end{array} ...\,\,\begin{array}{*{20}c} {({}^{i}{\varvec{d}}_{eH}^{c} )^{{\text{T}}} } & {({}^{i}{\varvec{d}}_{e1}^{s} )^{{\text{T}}} } & {({}^{i}{\varvec{d}}_{e2}^{s} )^{{\text{T}}} } \\ \end{array} ...\,\,\,({}^{i}{\varvec{d}}_{eH}^{s} )^{{\text{T}}} \}^{{\text{T}}} \hfill \\ \end{gathered}$$

(B.5)

Accordingly, Eq. (B.4) can be written in the form, which is given in Eq. (27). As an example, for $H = 1$, the forms of the matrices ${\varvec{D}}^{o}$, ${\varvec{D}}_{m}^{c}$ and $\,{\varvec{D}}_{m}^{s}$ ($m =$ 1, 2) and the vector (${}^{i}{\varvec{X}}_{e}$) are explicitly given in Eq. (B.6).

$$\begin{gathered} {\varvec{D}}^{o} = \left[ {\begin{array}{*{20}c} {({}^{i}{\varvec{d}}_{eI} )^{o} } & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{\varvec{d}}_{eI} )_{1}^{c} \,} & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{\varvec{d}}_{eI} )_{1}^{s} \,} \\ \end{array} } \right]\,, \hfill \\ {\varvec{D}}_{1}^{c} = \left[ {\begin{array}{*{20}c} {({}^{i}{\varvec{d}}_{eI} )_{1}^{c} \,} & {({}^{i}{\varvec{d}}_{eI} )^{o} \,} & {\varvec{O}} \\ \end{array} } \right],\;{\varvec{D}}_{2}^{c} = \left[ {\begin{array}{*{20}c} {\varvec{O}} & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{\varvec{d}}_{eI} )_{1}^{c} \,} & { - ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{\varvec{d}}_{eI} )_{1}^{s} } \\ \end{array} } \right] \hfill \\ {\varvec{D}}_{1}^{s} = \left[ {\begin{array}{*{20}c} {({}^{i}{\varvec{d}}_{eI} )_{1}^{s} \,} & {\varvec{O}} & {({}^{i}{\varvec{d}}_{eI} )^{o} } \\ \end{array} } \right],\;{\varvec{D}}_{2}^{s} = \left[ {\begin{array}{*{20}c} {\varvec{O}} & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})\,({}^{i}{\varvec{d}}_{eI} )_{1}^{s} } & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{\varvec{d}}_{eI} )_{1}^{c} } \\ \end{array} } \right] \hfill \\ {}^{i}{\varvec{X}}_{e} = \{ \begin{array}{*{20}c} {({}^{i}{\varvec{d}}_{e}^{o} )^{{\text{T}}} } & {({}^{i}{\varvec{d}}_{e1}^{c} )^{{\text{T}}} } & {({}^{i}{\varvec{d}}_{e1}^{s} )^{{\text{T}}} } \\ \end{array} \}^{{\text{T}}} \hfill \\ \end{gathered}$$

(B.6)

where ${\varvec{O}}$ is the null matrix of the size of $({}^{i}{\varvec{d}}_{eI} )^{o}$ or $({}^{i}{\varvec{d}}_{eI} )_{q}^{s}$ or $({}^{i}{\varvec{d}}_{eI} )_{q}^{c} \,$).

The Fourier expansion of the stress matrix ${}^{i}{{\varvec{\Gamma}}}^{k}$ can be written as

$${}^{i}{{\varvec{\Gamma}}}^{k} = ({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} + \sum\limits_{q = 1}^{2H} {({}^{i}{{\varvec{\Gamma}}}^{k} )_{q}^{c} \,\cos (q\omega t) + ({}^{i}{{\varvec{\Gamma}}}^{k} )_{q}^{s} \,\sin (q\omega t)}$$

(B.7)

where $({}^{i}{{\varvec{\Gamma}}}^{k} )^{o}$, $({}^{i}{{\varvec{\Gamma}}}^{k} )_{q}^{s} \,$ and $({}^{i}{{\varvec{\Gamma}}}^{k} )_{q}^{c}$ are the coefficient matrices for the constant, sine and cosine terms, respectively. Similarly, using the Fourier expansion of the nodal displacement vector (Eq. B.1), the expanded form of the linear strain vector $\Delta {{\varvec{\upvarepsilon}}}_{g}^{w}$ ($\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} = {\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{e}$, Eq. 25b) can be written as

$$\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} = {\varvec{B}}_{g}^{w} \Delta {\varvec{d}}_{e}^{o} + \sum\limits_{n = 1}^{H} {{\varvec{B}}_{g}^{w} \Delta {\varvec{d}}_{en}^{c} \,\cos (n\omega t) + {\varvec{B}}_{g}^{w} \Delta {\varvec{d}}_{en}^{s} \,\sin (n\omega t)}$$

(B.8)

where $\Delta {\varvec{d}}_{e}^{o}$, $\Delta {\varvec{d}}_{en}^{s}$ and $\Delta {\varvec{d}}_{en}^{c}$ are the amplitude vectors for the constant, sine and cosine terms, respectively, in the Fourier expansion of $\Delta {\varvec{d}}_{e}$. Using Eqs. (B.7) and (B.8), the product $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )$ can be formulated as

$${}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} = ({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} {\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{e}^{o} + \left\{ \begin{gathered} \sum\limits_{q = 1}^{H} {\left[ {({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} \,{\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{em}^{c} \cos (q\omega t) + ({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} \,{\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{em}^{s} \sin (q\omega t)} \right]} + \hfill \\ \hfill \\ \sum\limits_{q = 1}^{2H} {\left[ {({}^{i}{{\varvec{\Gamma}}}^{k} )_{m}^{c} \,{\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{e}^{o} \cos (q\omega t) + ({}^{i}{{\varvec{\Gamma}}}^{k} )_{m}^{s} \,{\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{e}^{o} \sin (q\omega t)} \right]} + \hfill \\ \sum\limits_{q = 1}^{2H} {\sum\limits_{n = 1}^{H} {\frac{1}{2}\left\{ \begin{gathered} \left[ {({}^{i}{{\varvec{\Gamma}}}^{k} )_{m}^{c} \,{\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{en}^{c} } \right]\left[ {\cos (q + n)\omega t + \cos (q - n)\omega t} \right] + \hfill \\ \left[ {({}^{i}{{\varvec{\Gamma}}}^{k} )_{m}^{s} \,{\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{en}^{s} } \right]\left[ {\cos (q - n)\omega t - \cos (q + n)\omega t} \right] + \hfill \\ \left[ {({}^{i}{{\varvec{\Gamma}}}^{k} )_{m}^{c} \,{\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{en}^{s} } \right]\left[ {\sin (q + n)\omega t - \sin (q - n)\omega t} \right] + \hfill \\ \left[ {({}^{i}{{\varvec{\Gamma}}}^{k} )_{m}^{s} \,{\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{en}^{c} } \right]\left[ {\sin (q + n)\omega t + \sin (q - n)\omega t} \right] \hfill \\ \end{gathered} \right\}\,} } \hfill \\ \end{gathered} \right\}$$

(B.9)

The expanded form of the product $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )$ can also be expressed in the conventional form of Fourier series as follows

$${}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} = ({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )^{o} + \sum\limits_{m = 1}^{3H} {({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )_{m}^{c} \cos (m\omega t) + ({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )_{m}^{s} \sin (m\omega t)}$$

(B.10)

where $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )^{o}$, $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )_{m}^{c} \,$ and $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )_{m}^{s} \,$) are the amplitude vectors for the constant, cosine and sine terms, respectively. Equations (B.9) and (B.10) show that an amplitude vector ($({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )^{o}$ or $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )_{m}^{c} \,$ or $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )_{m}^{s} \,$)) appears in terms of the coefficient matrices ($({}^{i}{{\varvec{\Gamma}}}^{k} )^{o}$, $({}^{i}{{\varvec{\Gamma}}}^{k} )_{q}^{s} \,$, $({}^{i}{{\varvec{\Gamma}}}^{k} )_{q}^{c}$) and displacement amplitude vectors ($\Delta {\varvec{d}}_{e}^{o}$, $\Delta {\varvec{d}}_{en}^{s}$ and $\Delta {\varvec{d}}_{en}^{c}$). So, the products $({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} {\varvec{B}}_{g}^{w}$, $({}^{i}{{\varvec{\Gamma}}}^{k} )_{m}^{s} {\varvec{B}}_{g}^{w}$ and $({}^{i}{{\varvec{\Gamma}}}^{k} )_{m}^{c} \,{\varvec{B}}_{g}^{w}$) in any amplitude vector ($({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )^{o}$ or $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )_{m}^{c} \,$ or $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} )_{m}^{s} \,$) are taken together within a matrix (${(}{\varvec{\varUpsilon}}_{w}^{k} )^{o}$ or $({\varvec{\varUpsilon}}_{w}^{k} )_{m}^{c}$ or $\,({\varvec{\varUpsilon}}_{w}^{k} )_{m}^{s}$), while the associated nodal displacement amplitude vectors ($\Delta {\varvec{d}}_{e}^{o}$, $\Delta {\varvec{d}}_{em}^{s}$ and $\Delta {\varvec{d}}_{em}^{c}$, $m = 1,\,\,2,\,\,3,...,H$) are taken in the form of a generalized nodal displacement amplitude vector ($\Delta {\varvec{X}}_{e}$) according to the following expressions

$$\begin{gathered} ({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} {)}^{o} { = }\,{(}{\varvec{\varUpsilon}}_{w}^{k} )^{o} \Delta {\varvec{X}}_{e} ,\;({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} {)}_{m}^{c} = \,{(}{\varvec{\varUpsilon}}_{w}^{k} )_{m}^{c} \Delta {\varvec{X}}_{e} ,\;({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} {)}_{m}^{s} { = }\,{(}{\varvec{\varUpsilon}}_{w}^{k} )_{m}^{s} \Delta {\varvec{X}}_{e} \hfill \\ \Delta {\varvec{X}}_{e} = \{ \begin{array}{*{20}c} {(\Delta {\varvec{d}}_{e}^{o} )^{{\text{T}}} } & {(\Delta {\varvec{d}}_{e1}^{c} )^{{\text{T}}} } & {(\Delta {\varvec{d}}_{e2}^{c} )^{{\text{T}}} } \\ \end{array} ...\,\,\begin{array}{*{20}c} {(\Delta {\varvec{d}}_{eH}^{c} )^{{\text{T}}} } & {(\Delta {\varvec{d}}_{e1}^{s} )^{{\text{T}}} } & {(\Delta {\varvec{d}}_{e2}^{s} )^{{\text{T}}} } \\ \end{array} ...\,\,\,(\Delta {\varvec{d}}_{eH}^{s} )^{{\text{T}}} \}^{{\text{T}}} \hfill \\ \end{gathered}$$

(B.11)

Accordingly, Eq. (B.10) is written in the form, as given in Eq. (32a). As an example, for $H = 1$, the forms of the matrices ${(}{\varvec{\varUpsilon}}_{w}^{k} )^{o}$, $({\varvec{\varUpsilon}}_{w}^{k} )_{m}^{c}$ and $\,({\varvec{\varUpsilon}}_{w}^{k} )_{m}^{s}$ are explicitly given in the following expressions

$$\begin{gathered} ({\varvec{\varUpsilon}}_{w}^{k} )^{o} = \left[ {\begin{array}{*{20}c} {({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} {\varvec{B}}_{g}^{w} } & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{1}^{c} {\varvec{B}}_{g}^{w} \,} & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{1}^{s} {\varvec{B}}_{g}^{w} \,} \\ \end{array} } \right]\,, \hfill \\ ({\varvec{\varUpsilon}}_{w}^{k} )_{1}^{c} = \left[ {\begin{array}{*{20}c} {({}^{i}{{\varvec{\Gamma}}}^{k} )_{1}^{c} {\varvec{B}}_{g}^{w} \,} & {\left\{ {({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} + ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{c} } \right\}{\varvec{B}}_{g}^{w} \,} & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{s} {\varvec{B}}_{g}^{w} } \\ \end{array} } \right], \hfill \\ ({\varvec{\varUpsilon}}_{w}^{k} )_{2}^{c} = \left[ {\begin{array}{*{20}c} {({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{c} {\varvec{B}}_{g}^{w} } & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{1}^{c} {\varvec{B}}_{g}^{w} \,} & { - ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{1}^{s} {\varvec{B}}_{g}^{w} } \\ \end{array} } \right], \hfill \\ ({\varvec{\varUpsilon}}_{w}^{k} )_{3}^{c} = \left[ {\begin{array}{*{20}c} {\varvec{O}} & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{c} {\varvec{B}}_{g}^{w} \,} & { - ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{s} {\varvec{B}}_{g}^{w} } \\ \end{array} } \right], \hfill \\ ({\varvec{\varUpsilon}}_{w}^{k} )_{1}^{s} = \left[ {\begin{array}{*{20}c} {({}^{i}{{\varvec{\Gamma}}}^{k} )_{1}^{s} {\varvec{B}}_{g}^{w} \,} & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{s} {\varvec{B}}_{g}^{w} } & {\left\{ {({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} - ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{c} } \right\}{\varvec{B}}_{g}^{w} } \\ \end{array} } \right], \hfill \\ ({\varvec{\varUpsilon}}_{w}^{k} )_{2}^{s} = \left[ {\begin{array}{*{20}c} {({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{s} {\varvec{B}}_{g}^{w} } & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})\,({}^{i}{{\varvec{\Gamma}}}^{k} )_{1}^{s} {\varvec{B}}_{g}^{w} } & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{1}^{c} {\varvec{B}}_{g}^{w} } \\ \end{array} } \right], \hfill \\ ({\varvec{\varUpsilon}}_{w}^{k} )_{3}^{s} = \left[ {\begin{array}{*{20}c} {\varvec{O}} & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})\,({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{s} {\varvec{B}}_{g}^{w} } & {({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2})({}^{i}{{\varvec{\Gamma}}}^{k} )_{2}^{c} {\varvec{B}}_{g}^{w} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$

(B.12)

where ${\varvec{O}}$ is the null matrix of the same size of $({}^{i}{{\varvec{\Gamma}}}^{k} )^{o} {\varvec{B}}_{g}^{w}$. The above expressions can also be used for the expanded form of the product $({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} )$, where ${\varvec{B}}_{g}^{w}$ is to be replaced by ${\varvec{B}}_{g}^{u}$ since $\Delta {{\varvec{\upvarepsilon}}}_{g}^{u}$ ($\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} = {\varvec{B}}_{g}^{u} \,\Delta {\varvec{d}}_{e}$, Eq. (25b)) is involved instead of $\Delta {{\varvec{\upvarepsilon}}}_{g}^{w}$ ($\Delta {{\varvec{\upvarepsilon}}}_{g}^{w} = {\varvec{B}}_{g}^{w} \,\Delta {\varvec{d}}_{e}$, Eq. (25b)). So, in this case, Eqs. (B.10) and (B.11) can be modified as

$$\begin{gathered} {}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} = ({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} )^{o} + \sum\limits_{m = 1}^{3H} {({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} )_{m}^{c} \cos (m\omega t) + ({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} )_{m}^{s} \sin (m\omega t)} \hfill \\ ({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} {)}^{o} { = }\,{(}{\varvec{\varUpsilon}}_{u}^{k} )^{o} \Delta {\varvec{X}}_{e} ,\;({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} {)}_{m}^{c} { = }\,{(}{\varvec{\varUpsilon}}_{u}^{k} )_{m}^{c} \Delta {\varvec{X}}_{e} ,\;({}^{i}{{\varvec{\Gamma}}}^{k} \,\Delta {{\varvec{\upvarepsilon}}}_{g}^{u} {)}_{m}^{s} { = }\,{(}{\varvec{\varUpsilon}}_{u}^{k} )_{m}^{s} \Delta {\varvec{X}}_{e} \hfill \\ \end{gathered}$$

(B.13)

where the form of $\Delta {\varvec{X}}_{e}$ remains the same as given in Eq. (B.11). Equation (B.13) is written in the form, as given in Eq. (32b).

Appendix C

The fractional Zener model for a viscoelastic material with the frequency-dependent Poisson’s ratio can be written as [42]

$$\begin{gathered} {{\varvec{\upsigma}}}_{a} + \tau_{a}^{\alpha } \,({{d^{\alpha } {{\varvec{\upsigma}}}_{a} } \mathord{\left/ {\vphantom {{d^{\alpha } {{\varvec{\upsigma}}}_{a} } {dt^{\alpha } }}} \right. \kern-0pt} {dt^{\alpha } }}) = 3\left[ {K_{o} {{\varvec{\upvarepsilon}}}_{a} + K_{\infty } \tau_{a}^{\alpha } \,({{d^{\alpha } {{\varvec{\upvarepsilon}}}_{a} } \mathord{\left/ {\vphantom {{d^{\alpha } {{\varvec{\upvarepsilon}}}_{a} } {dt^{\alpha } }}} \right. \kern-0pt} {dt^{\alpha } }})} \right] \hfill \\ {{\varvec{\upsigma}}}_{d} + \tau_{d}^{\beta } \,({{d^{\beta } {{\varvec{\upsigma}}}_{d} } \mathord{\left/ {\vphantom {{d^{\beta } {{\varvec{\upsigma}}}_{d} } {dt^{\beta } }}} \right. \kern-0pt} {dt^{\beta } }}) = 2\left[ {G_{o} {{\varvec{\upvarepsilon}}}_{d} + G_{\infty } \tau_{d}^{\beta } \,({{d^{\beta } {{\varvec{\upvarepsilon}}}_{d} } \mathord{\left/ {\vphantom {{d^{\beta } {{\varvec{\upvarepsilon}}}_{d} } {dt^{\beta } }}} \right. \kern-0pt} {dt^{\beta } }})} \right] \hfill \\ \end{gathered}$$

(C.1a)

$$\begin{gathered} {{\varvec{\upsigma}}}_{a} = \left\{ {\begin{array}{*{20}c} p & p & p & 0 & 0 & 0 \\ \end{array} } \right\}^{{\text{T}}} ,\;{{\varvec{\upvarepsilon}}}_{a} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{v} } & {\varepsilon_{v} } & {\varepsilon_{v} } & 0 & 0 & 0 \\ \end{array} } \right\}^{{\text{T}}} , \hfill \\ {{\varvec{\upsigma}}}_{d} = \left\{ {\begin{array}{*{20}c} {\sigma_{x} - p} & {\sigma_{y} - p} & {\sigma_{z} - p} & {\tau_{yz} } & {\tau_{zx} } & {\tau_{xy} } \\ \end{array} } \right\}^{{\text{T}}} , \hfill \\ {{\varvec{\upvarepsilon}}}_{d} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} - \varepsilon_{v} } & {\varepsilon_{y} - \varepsilon_{v} } & {\varepsilon_{z} - \varepsilon_{v} } & {(1/2)\gamma_{yz} } & {(1/2)\gamma_{zx} } & {(1/2)\gamma_{xy} } \\ \end{array} } \right\}^{{\text{T}}} , \hfill \\ p = {{\left( {\sigma_{x} + \sigma_{y} + \sigma_{z} } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{x} + \sigma_{y} + \sigma_{z} } \right)} 3}} \right. \kern-0pt} 3},\;\varepsilon_{v} = {{\left( {\varepsilon_{x} + \varepsilon_{y} + \varepsilon_{z} } \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon_{x} + \varepsilon_{y} + \varepsilon_{z} } \right)} 3}} \right. \kern-0pt} 3} \hfill \\ \end{gathered}$$

(C.1b)

where ${{\varvec{\upsigma}}}_{a}$/${{\varvec{\upvarepsilon}}}_{a}$ and ${{\varvec{\upsigma}}}_{d}$/${{\varvec{\upvarepsilon}}}_{d}$ are the volumetric and deviatoric parts of stress/strain, respectively, as given in Eq. (C.1b); the subscript $x$/$y$/$z$ indicates the normal stress/strain components along the $x$/$y$/$z$ direction in the reference Cartesian coordinate system ($xyz$); the subscript $yz$/$zx$/$xy$ indicates the shear stress/strain in the $yz$/$zx$/$xy$ plane of the reference Cartesian coordinate system ($xyz$); ${{K_{o} } \mathord{\left/ {\vphantom {{K_{o} } {G_{o} }}} \right. \kern-0pt} {G_{o} }}$ and ${{K_{\infty } } \mathord{\left/ {\vphantom {{K_{\infty } } {G_{\infty } }}} \right. \kern-0pt} {G_{\infty } }}$ are the relaxed and non-relaxed bulk/shear moduli, respectively; ${{\tau_{a}^{\alpha } } \mathord{\left/ {\vphantom {{\tau_{a}^{\alpha } } {\tau_{d}^{\beta } }}} \right. \kern-0pt} {\tau_{d}^{\beta } }}$ and ${\alpha \mathord{\left/ {\vphantom {\alpha \beta }} \right. \kern-0pt} \beta }$ are the relaxation time and the fractional-order time derivative, respectively, for the volumetric/deviatoric constitutive relation. Here, the volumetric and deviatoric constitutive relations (Eq. C.1a) appear similar to that given in Eq. (13). Therefore, each of these constitutive relations (Eq. C.1a) can be reduced for the periodic stress/strain following the same procedure as described in Sect. 3.1. The resulting expressions can be written as

$$\begin{gathered} {{\varvec{\upsigma}}}_{a} = 3K_{o} \,{{\varvec{\upvarepsilon}}}_{a}^{t} \hfill \\ {{\varvec{\upvarepsilon}}}_{a}^{t} = ({{\varvec{\upvarepsilon}}}_{a} )^{o} + \sum\limits_{m = 1}^{H} {\left\{ {f_{am}^{c} ({{\varvec{\upvarepsilon}}}_{a} )_{m}^{c} + f_{am}^{s} ({{\varvec{\upvarepsilon}}}_{a} )_{m}^{s} } \right\}\cos (m\omega t) + \left\{ {f_{am}^{c} ({{\varvec{\upvarepsilon}}}_{a} )_{m}^{s} - f_{am}^{s} ({{\varvec{\upvarepsilon}}}_{a} )_{m}^{c} } \right\}\sin (m\omega t)} \hfill \\ f_{am}^{c} = ({{K_{\infty } } \mathord{\left/ {\vphantom {{K_{\infty } } {K_{o} )}}} \right. \kern-0pt} {K_{o} )}}\left[ {1 - f_{am} \left\{ {1 + c_{al} \,(m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}} \right],\;f_{am}^{s} = ({{K_{\infty } } \mathord{\left/ {\vphantom {{K_{\infty } } {K_{o} )}}} \right. \kern-0pt} {K_{o} )}}f_{am} \,s_{al} \,(m\omega \tau_{a}^{\alpha } )^{\alpha } \hfill \\ f_{am} = {{f_{a} } \mathord{\left/ {\vphantom {{f_{a} } {\left[ {\left\{ {1 + c_{al} (m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}^{2} + \left\{ {s_{al} \,(m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}^{2} } \right]}}} \right. \kern-0pt} {\left[ {\left\{ {1 + c_{al} (m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}^{2} + \left\{ {s_{al} \,(m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}^{2} } \right]}} \hfill \\ c_{al} = \cos ({{\pi \alpha } \mathord{\left/ {\vphantom {{\pi \alpha } 2}} \right. \kern-0pt} 2}),\,\,s_{al} = \sin ({{\pi \alpha } \mathord{\left/ {\vphantom {{\pi \alpha } 2}} \right. \kern-0pt} 2}),\;f_{a} = {{(K_{\infty } - K_{o} )} \mathord{\left/ {\vphantom {{(K_{\infty } - K_{o} )} {K_{\infty } }}} \right. \kern-0pt} {K_{\infty } }} \hfill \\ \end{gathered}$$

(C.2a)

$$\begin{gathered} {{\varvec{\upsigma}}}_{a} = 3K_{o} \,{{\varvec{\upvarepsilon}}}_{a}^{t} \hfill \\ {{\varvec{\upvarepsilon}}}_{a}^{t} = ({{\varvec{\upvarepsilon}}}_{a} )^{o} + \sum\limits_{m = 1}^{H} {\left\{ {f_{am}^{c} ({{\varvec{\upvarepsilon}}}_{a} )_{m}^{c} + f_{am}^{s} ({{\varvec{\upvarepsilon}}}_{a} )_{m}^{s} } \right\}\cos (m\omega t) + \left\{ {f_{am}^{c} ({{\varvec{\upvarepsilon}}}_{a} )_{m}^{s} - f_{am}^{s} ({{\varvec{\upvarepsilon}}}_{a} )_{m}^{c} } \right\}\sin (m\omega t)} \hfill \\ f_{am}^{c} = ({{K_{\infty } } \mathord{\left/ {\vphantom {{K_{\infty } } {K_{o} )}}} \right. \kern-0pt} {K_{o} )}}\left[ {1 - f_{am} \left\{ {1 + c_{al} \,(m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}} \right],\;f_{am}^{s} = ({{K_{\infty } } \mathord{\left/ {\vphantom {{K_{\infty } } {K_{o} )}}} \right. \kern-0pt} {K_{o} )}}f_{am} \,s_{al} \,(m\omega \tau_{a}^{\alpha } )^{\alpha } \hfill \\ f_{am} = {{f_{a} } \mathord{\left/ {\vphantom {{f_{a} } {\left[ {\left\{ {1 + c_{al} (m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}^{2} + \left\{ {s_{al} \,(m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}^{2} } \right]}}} \right. \kern-0pt} {\left[ {\left\{ {1 + c_{al} (m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}^{2} + \left\{ {s_{al} \,(m\omega \tau_{a}^{\alpha } )^{\alpha } } \right\}^{2} } \right]}} \hfill \\ c_{al} = \cos ({{\pi \alpha } \mathord{\left/ {\vphantom {{\pi \alpha } 2}} \right. \kern-0pt} 2}),\,\,s_{al} = \sin ({{\pi \alpha } \mathord{\left/ {\vphantom {{\pi \alpha } 2}} \right. \kern-0pt} 2}),\;f_{a} = {{(K_{\infty } - K_{o} )} \mathord{\left/ {\vphantom {{(K_{\infty } - K_{o} )} {K_{\infty } }}} \right. \kern-0pt} {K_{\infty } }} \hfill \\ \end{gathered}$$

(C.2b)

The total stress can be obtained by the addition of deviatoric (Eq. C.2b) and volumetric (Eq. C.2a) counterparts of stress. Introducing the stress/strain components (Eq. C.1b) in the expression of this total stress (${\varvec{\sigma}} = {\varvec{\sigma}}_{a} + {\varvec{\sigma}}_{d}$), the constitutive relation for one of the stress components, say $\sigma_{x}$, can be written as

$$\begin{aligned} {{\varvec{\upsigma}}}_{x} & = K_{o} \left[ {({{\varvec{\upvarepsilon}}}_{x} + {{\varvec{\upvarepsilon}}}_{y} + {{\varvec{\upvarepsilon}}}_{z} )^{o} + \sum\limits_{m = 1}^{H} {\left\{ \begin{gathered} \left[ {f_{am}^{c} ({{\varvec{\upvarepsilon}}}_{x} + {{\varvec{\upvarepsilon}}}_{y} + {{\varvec{\upvarepsilon}}}_{z} )_{m}^{c} + f_{am}^{s} ({{\varvec{\upvarepsilon}}}_{x} + {{\varvec{\upvarepsilon}}}_{y} + {{\varvec{\upvarepsilon}}}_{z} )_{m}^{s} } \right]\cos (m\omega t) \hfill \\ + \left[ {f_{am}^{c} ({{\varvec{\upvarepsilon}}}_{x} + {{\varvec{\upvarepsilon}}}_{y} + {{\varvec{\upvarepsilon}}}_{z} )_{m}^{s} - f_{am}^{s} ({{\varvec{\upvarepsilon}}}_{x} + {{\varvec{\upvarepsilon}}}_{y} + {{\varvec{\upvarepsilon}}}_{z} )_{m}^{c} } \right]\sin (m\omega t) \hfill \\ \end{gathered} \right\}} } \right] \\ & \quad + \frac{{2\,G_{o} }}{3}\,\left[ {(2{{\varvec{\upvarepsilon}}}_{x} - {{\varvec{\upvarepsilon}}}_{y} - {{\varvec{\upvarepsilon}}}_{z} )^{o} + \sum\limits_{m = 1}^{H} {\left\{ \begin{gathered} \left[ {f_{dm}^{c} (2{{\varvec{\upvarepsilon}}}_{x} - {{\varvec{\upvarepsilon}}}_{y} - {{\varvec{\upvarepsilon}}}_{z} )_{m}^{c} + f_{dm}^{s} (2{{\varvec{\upvarepsilon}}}_{x} - {{\varvec{\upvarepsilon}}}_{y} - {{\varvec{\upvarepsilon}}}_{z} )_{m}^{s} } \right]\cos (m\omega t) \hfill \\ + \left[ {f_{dm}^{c} (2{{\varvec{\upvarepsilon}}}_{x} - {{\varvec{\upvarepsilon}}}_{y} - {{\varvec{\upvarepsilon}}}_{z} )_{m}^{s} - f_{dm}^{s} (2{{\varvec{\upvarepsilon}}}_{x} - {{\varvec{\upvarepsilon}}}_{y} - {{\varvec{\upvarepsilon}}}_{z} )_{m}^{c} } \right]\sin (m\omega t) \hfill \\ \end{gathered} \right\}} } \right] \\ \end{aligned}$$

(C.3)

The other stress components also appear with the similar expression as given in Eq. (C.3) for $\sigma_{x}$. If all stress components are taken in the conventional form of stress vector, then the overall reduced constitutive relation can be written as

$$\begin{gathered} {{\varvec{\upsigma}}} = ({\varvec{C}}_{a} \,\,{}^{t}{{\varvec{\upvarepsilon}}}_{a} + {\varvec{C}}_{d} \,\,{}^{t}{{\varvec{\upvarepsilon}}}_{d} ) \hfill \\ {}^{t}{{\varvec{\upvarepsilon}}}_{a} = ({{\varvec{\upvarepsilon}}})^{o} + \sum\limits_{m = 1}^{H} {\left\{ {\left[ {f_{am}^{c} ({{\varvec{\upvarepsilon}}})_{m}^{c} + f_{am}^{s} ({{\varvec{\upvarepsilon}}})_{m}^{s} } \right]\cos (m\omega t) + \left[ {f_{am}^{c} ({{\varvec{\upvarepsilon}}})_{m}^{s} - f_{am}^{s} ({{\varvec{\upvarepsilon}}})_{m}^{c} } \right]} \right\}\sin (m\omega t)} , \hfill \\ {\varvec{C}}_{a} = K_{o} \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\;{\varvec{C}}_{d} = \frac{{2\,G_{o} }}{3}\left[ {\begin{array}{*{20}c} 2 & { - 1} & { - 1} & 0 & 0 & 0 \\ { - 1} & 2 & { - 1} & 0 & 0 & 0 \\ { - 1} & { - 1} & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} \\ \end{array} } \right] \hfill \\ {{\varvec{\upsigma}}} = \left\{ {\begin{array}{*{20}c} {\sigma_{x} } & {\sigma_{y} } & {\sigma_{z} } & {\tau_{yz} } & {\tau_{zx} } & {\tau_{xy} } \\ \end{array} } \right\}^{{\text{T}}} \hfill \\ {{\varvec{\upvarepsilon}}} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } & {\varepsilon_{y} } & {\varepsilon_{z} } & {\gamma_{yz} } & {\gamma_{zx} } & {\gamma_{xy} } \\ \end{array} } \right\}^{{\text{T}}} \hfill \\ \end{gathered}$$

(C.4)

This reduced constitutive relation (Eq. C.4) appears in the similar form of that in Eqs. (15a–15b), where the only difference appears as the involvement of two stiffness matrices (${\varvec{C}}_{a} \,,\;{\varvec{C}}_{d}$) because of the consideration of volumetric and deviatoric parts of stress/strain.