On the reliability, consistency, and method-specificity based on the CT-C(M–1) model

Abstract

In the present study, we discuss reliability, consistency, and method specificity based on the CT-C(M − 1) model, which provides clear definitions of trait and method factors and can facilitate parameter estimation. Properties of the reliability coefficient, the consistency coefficient, and the method-specificity coefficient of the summated score for a trait factor are addressed. The consistency coefficient and the method-specificity coefficient are both functions of the number of items, the average item consistency, and the average item method specificity. The usefulness of the findings is demonstrated in an alternative approach proposed for scale reduction. The approach, taking into account both traits and methods, helps identify the items leading to the maximum of convergent validity or method effects. The approach, illustrated with a simulated data set, is recommended for scale development based on multitrait–multimethod designs.

Multitrait-multimethod (MTMM) analysis, proposed by Campbell and Fiske (1959), has become an essential strategy for examining the construct validity of psychological measures (Eid & Diener, 2006). In MTMM designs, each of several traits (constructs) is measured by each of several methods. For example, in Mount’s (1984) study, the traits of administrative ability, ability to give feedback to subordinates, and consideration when dealing with others were measured by using the three methods: self-rating, supervisor rating, and subordinate rating. Convergent validity is supported when different methods yield consistent results in measuring the same trait. Discriminant validity is supported when the traits can be well distinguished from each other.

Confirmatory factor analysis (CFA) is the analytical approach that is most consistent with Campbell and Fiske’s (1959) original formulation of the MTMM matrix (e.g., Lance, Noble, & Scullen, 2002; Schmitt & Stults, 1986; Widaman, 1985). The effects of all traits and all methods are examined simultaneously in MTMM–CFA models. Therefore, convergent and discriminant validities are assessed in the presence of method effects. Controlling for method effects can reduce potential bias in parameter estimates. Widaman proposed hierarchically nested CFA models for MTMM data to facilitate examining trait and method effects. Although trait effects reflect how well a measure can represent its underlying trait, method effects reflect how much it is affected by the measurement method. The amount of method effects differs greatly across disciplines (Cote & Buckley, 1987; Malhotra, Kim, & Patil, 2006; Mishra, 2000).

A well-known MTMM–CFA model is the correlated trait-correlated method (CT–CM) model, in which all traits to be studied are regarded as trait factors and all methods that are applied are regarded as method factors. The trait factors can covary among themselves, and the method factors can covary among themselves as well. However, trait and method factors are assumed to be uncorrelated. In addition, it is assumed that method factors do not interact with trait factors. Although the CT–CM model is faithful to Campbell and Fiske’s (1959) original theoretical formulation of the MTMM matrix, this model suffers from two disadvantages. First, estimation problems often occur, especially when method factors are correlated (e.g., Kenny & Kashy, 1992; Marsh, 1989; Marsh & Grayson, 1995), although using larger MTMM matrices (i.e., more traits and methods) together with larger samples may yield admissible solutions (Conway, Lievens, Scullen, & Lance, 2004; Marsh & Bailey, 1991). Second, neither the trait factors nor the method factors are clearly defined, making their interpretation difficult (Eid, Lischetzke, Nussbeck, & Trierweiler, 2003; Pohl, Steyer, & Kraus, 2008). To improve the model, Eid (2000) and Eid et al. (2003) recommended the CT-C(M − 1) model. It is named CT-C(M − 1) because the number of method factors is one less than the number of methods used. At first, one method, called the standard (or reference) method, has to be chosen as the comparison standard. Then, for each trait, the true score of an item measured by the standard method is taken as a predictor. The method variable for an item measured by a nonstandard method is the residual resulting from the regression of the item true score on the predictor. It is assumed that the method variables associated with the same nonstandard method are homogeneous, having a common method factor. The common method factor thus captures reliable residual effects that are specific to the items measured by that nonstandard method and are not shared with the items measured by the standard method. Three important consequences follow. The first one is the absence of the method factor for the standard method, and therefore the trait is confounded with the standard method. The second one is the uncorrelatedness of trait and method factors, allowing the estimation of variance components due to trait, method, and error effects for the items measured by nonstandard methods. The third one is that the method factors can be correlated. This correlation is a partial correlation. The CT-C(M − 1) model avoids the estimation problems inherent in the CT–CM model. However, the parameter estimates depend on the standard method chosen. The meaning of the trait factor varies with different standard methods. The choice of the standard method should be guided by the research question and substantive theory (Geiser, Eid, & Nussbeck, 2008).

Decomposition of the reliability coefficient into the consistency coefficient and the method-specificity coefficient based on MTMM models can be seen in the literature (e.g., Deinzer et al., 1995; Eid, 2000; Eid et al., 2003; Schmitt & Steyer, 1993). When trait factors, method factors, and errors are uncorrelated, the variance of an item can be decomposed into trait variance, method variance, and error variance. The reliability coefficient of the item is that part of the item variance explained by the trait and method factors. It is the part of variance that is not due to measurement error. The consistency coefficient represents the proportion of the item variance due to the trait factor. The method-specificity coefficient represents the proportion of the item variance due to the measurement method. The reliability coefficient is the sum of the consistency coefficient and the method-specificity coefficient. The consistency coefficient is a quantitative indicator of convergent validity (Eid 2000; Eid et al., 2003). Deinzer et al. (1995) mentioned that, the consistency coefficient rather than the reliability coefficient should be used for examining trait effects.

It is usually of interest in behavior studies to assess reliability of the sum of items in a scale. Analyses of reliability, consistency, and method specificity for the sum of items across different methods based on an MTMM design become more complex. As can be seen later, the reliability of the summated score for a trait factor is a joint function of the average item reliability and scale length (the number of items used to measure the trait factor), regardless of whether there exist method factors in the model. However, the consistency coefficient and the method-specificity coefficient—the two components of the reliability coefficient—of the summated score possess somewhat different properties, which are important when assessing the quality of a scale under MTMM designs. Relevant discussions seem not addressed in the literature. The purpose of the present study was to fill this gap. The findings will be useful for behavior researchers conducting MTMM studies.

Reliability as a function of the number of items

In classical test theory (CTT), ${x_{{ij}}} = {t_{{ij}}} + {\varepsilon_{{ij}}},\;i = 1,\;...,\;I;j = 1,\;...,\;{J_i}$, where x _ij denotes the observed score on the jth item for the ith trait factor, t _ij is its true score, ε _ij is the corresponding error, I is the number of trait factors in the model, and J _i is the number of items for measuring the ith trait factor. For congeneric items, true scores on different items for a trait factor are linearly related. Centered by its mean μ _ij , item x _ij can be formulated by CFA as (McDonald, 1999, p. 78)

$$ {x_{{ij}}} - {\mu_{{ij}}} = {\lambda_{{{F_{{ij}}}}}}{F_i} + {\varepsilon_{{ij}}},\;i = 1,\;...,\;I;\;j = 1,\;...,\;{J_i}, $$

(1)

where F _i denotes the latent factor for trait i, and ${\lambda_{{{F_{{ij}}}}}}$ is the trait loading of x _ij on F _i . ${\lambda_{{{F_{{ij}}}}}}$ is the covariance of x _ij and F _i . It is assumed that ${\sigma_{{{F_i}{\varepsilon_{{ij}}}}}} = 0$ and ${\sigma_{{{\varepsilon_{{ij}}}{\varepsilon_{{i\prime j\prime }}}}}} = 0{ }(i \ne i\prime \;{\text{or}}\;j \ne j\prime )$. For identification reasons, we usually set $\sigma_{{{F_i}}}^2 = 1$ or ${\lambda_{{{F_{{i1}}}}}} = 1$. The reliability of the summated score ${X_i} = \sum\limits_{{j = 1}}^{{{J_i}}} {{x_{{ij}}}}$ for trait F _i , denoted by $re{l_{{{F_i}}}}$ and defined as $re{l_{{{F_i}}}} = \sigma_{{{T_i}}}^2/\sigma_{{{X_i}}}^2$, where ${T_i} = \sum\limits_{{j = 1}}^{{{J_i}}} {{t_{{ij}}}} = \sum\limits_{{j = 1}}^{{{J_i}}} {{\lambda_{{ij}}}} {F_i}$, is then given by (Lord & Novick, 1968, Chap. 9)

$$ re{l_{{{F_i}}}} = \frac{{{{\left( {\sum\limits_{{j = 1}}^{{{J_i}}} {{\lambda_{{{F_{{ij}}}}}}} } \right)}^2}}}{{{{\left( {\sum\limits_{{j = 1}}^{{{J_i}}} {{\lambda_{{{F_{{ij}}}}}}} } \right)}^2} + \sum\limits_{{j = 1}}^{{{J_i}}} {\sigma_{{{\varepsilon_{{ij}}}}}^2} }}. $$

(2)

$re{l_{{{F_i}}}}$ is the proportion of the variance of X _i explained by F _i , and can be reexpressed as

$$ re{l_{{{F_i}}}} = \frac{{{J_i}{{\bar{\theta }}_{{{F_i}}}}}}{{1 + ({J_i} - 1){{\bar{\theta }}_{{{F_i}}}}}}, $$

(3)

where ${\bar{\theta }_{{{F_i}}}} = \frac{{{{\left( {{{\bar{\lambda }}_{{{F_i}}}}} \right)}^2}}}{{{{\left( {{{\bar{\lambda }}_{{{F_i}}}}} \right)}^2} + \overline {\sigma_{{{\varepsilon_i}}}^2} }}$, ${\bar{\lambda }_{{{F_i}}}} = \sum\limits_{{j = 1}}^{{{J_i}}} {{\lambda_{{{F_{{ij}}}}}}} /{J_i}$, $\overline {\sigma_{{{\varepsilon_i}}}^2} = \sum\limits_{{j = 1}}^{{{J_i}}} {\sigma_{{{\varepsilon_{{ij}}}}}^2/{J_i}}$, and $0 \leqslant {\bar{\theta }_{{{F_i}}}} \leqslant 1$. The reliability of the individual item x _ij for trait F _i is ${\theta_{{{x_{{ij}}}}}} = \lambda_{{{F_{{ij}}}}}^2/(\lambda_{{{F_{{ij}}}}}^2 + \sigma_{{{\varepsilon_{{ij}}}}}^2)$, j = 1, … , J _i , which is the proportion of its variance explained by F _i . Rather than the average variance extracted, given by $\overline {\lambda_{{{F_i}}}^2} /\left( {\overline {\lambda_{{{F_i}}}^2} + \overline {\sigma_{{{\varepsilon_i}}}^2} } \right)$ (where $\overline {\lambda_{{{F_i}}}^2} = \sum\limits_{{j = 1}}^{{{J_i}}} {\lambda_{{{F_{{ij}}}}}^2} /{J_i}$) (Fornell & Larcker, 1981), ${\bar{\theta }_{{{F_i}}}}$ is defined as the average item reliability for F _i (McDonald, 1999, p. 125), and is actually the reliability adjusted for scale length. $re{l_{{{F_i}}}}$ is a joint function of ${\bar{\theta }_{{{F_i}}}}$ and J _i (McDonald, 1999, p. 124). For a fixed value of ${\bar{\theta }_{{{F_i}}}}$, $re{l_{{{F_i}}}}$ increases as a function of J _i . The properties are similar in that coefficient alpha is a joint function of the average interrelatedness among items and the number of items (e.g., Cortina, 1993). An estimate of the item reliability ${\theta_{{{x_{{ij}}}}}}$, resulting from CFA, can serve as an index for assessing the internal quality of item j for trait i. A trait is “abstract” if it is reflected in a series of mental or physical activities (Bergkvist & Rossiter, 2007, p. 183). Scales for less abstract traits are usually composed of fewer items, with higher item reliabilities. On the other hand, for more abstract traits, more items with lower item reliabilities are needed. Although both can achieve a required level of reliability (e.g., .7), the former has fewer items but a greater $\bar{\theta }$ than the latter. When $\bar{\theta }$ is small, more items are needed to reach a desired reliability. Adding an item with lower item reliability will reduce $\bar{\theta }$, but may increase rel. Dropping an item with lower item reliability will increase $\bar{\theta }$, but may decrease rel.

Reliability, consistency, and method-specificity based on the CT-C(M−1) model

For MTMM data, items are affected not only by their underlying trait factors but also the measurement methods. Let x _ijk denote the observed score of the jth item for trait F _i with method M _k . The CFA model in Eq. 1 can be extended to formulate a CT–CM or a CT-C(M − 1) model, in which every trait is measured using every method with either a single item or multiple items. In the CT–CM model, every item loads on a trait factor and on a method factor. In the CT-C(M − 1) model, however, all items belonging to the standard method load exclusively on a trait factor. There is no method factor for these items (Eid et al., 2003; Geiser et al., 2008). If the first method (k = 1) is chosen as the standard method, the basic equations of the CT-C(M − 1) model are as follows:

$$ \begin{array}{*{20}{c}} {{x_{{ij1}}} = {t_{{ij1}}} + {\delta_{{ij1}}} = {\mu_{{ij1}}} + {\lambda_{{{F_{{ij1}}}}}}{F_{{i\_1}}} + {\delta_{{ij1}}}\;({\text{for}}\;{\text{the}}\;{\text{standard}}\;{\text{method}}\;(k = 1{)}),} \hfill \\ {{x_{{ijk}}} = {t_{{ijk}}} + {\delta_{{ijk}}} = {\mu_{{ijk}}} + {\lambda_{{{F_{{ijk}}}}}}{F_{{i\_1}}} + {\lambda_{{{M_{{ijk}}}}}}{M_k} + {\delta_{{ijk}}},\;i = 1,\;...,\;I,\;j = 1,\;...,\;{J_{{ik}}},k = 2, \ldots K,} \hfill \\ \end{array} $$

(4)

where t _ijk denotes the true score of x _ijk ; μ _ijk denotes the mean of x _ijk ; F _{i_1} denotes the ith trait factor measured by the first method, chosen as the standard method; M _k (k > 1) denotes the kth method factor; ${\lambda_{{{F_{{ijk}}}}}}$ denotes the trait loading of x _ijk on F _{i_1}; ${\lambda_{{{M_{{ijk}}}}}}$ denotes the method loading of x _ijk on M _k (k > 1); δ _ijk denotes the corresponding error; and J _ik denotes the number of items for measuring F _{i_1} with M _k . There are different ways (e.g., by fixing the variances of F _{i_1} and M _k to 1 [Geiser et al., 2008] or by fixing one loading per factor to 1 [and freely estimating the factor variances] [Eid et al., 2003]) to identify the model. In the present study, the factor variances are fixed to 1 because loadings represent trait and method effects to be assessed, and one would not want to give fixed values for them. It is assumed that $E({F_{{i\_1}}}) = E({M_k}) = 0$, ${\sigma_{{{F_{{i\_1}}}{\delta_{{ijk}}}}}} = 0$, $\sigma_{{{M_k}{\delta_{{ijk}}}}} = 0$, and ${\sigma_{{{\delta_{{ijk}}}{\delta_{{i\prime j\prime k\prime }}}}}} = 0\;(i \ne i\prime \;{\text{or}}\;j \ne j\prime \;{\text{or}}\;k \ne k\prime )$. In addition, traits and methods do not interact. Trait factors are allowed to covary, and method factors are allowed to covary as well. Without loss of generality, a CT-C(M − 1) model with the first method as the standard method for an MTMM design with three traits (F ₂, F ₃, F ₄) and three methods is illustrated in Fig. 1. x ₂₁₁, x ₂₁₂, and x ₂₁₃ are the items for measuring trait F ₂ by using methods 1, 2, and 3, respectively. x ₃₁₁, x ₃₂₁, x ₃₁₂, x ₃₂₂, x ₃₃₂, x ₃₁₃, and x ₃₂₃ are the items for measuring trait F ₃ by using the first method for the first two items, the second method for the middle three items, and the third method for the last two items. x ₄₁₁, x ₄₁₂, x ₄₁₃, and x ₄₂₃ are the items for measuring trait F ₄ by using the first method for the first item, the second method for the second item, and the third method for the last two items. M ₁ is missing in the figure because it is used as the standard method. F ₂, F ₃, and F ₄ are therefore the trait factors measured by the standard method (the first method). In the CT-C(M − 1) model, the three trait factors are better denoted by F _{2_1}, F _{3_1}, and F _{4_1} to make clear that they are specific to the first method.

Fig. 1

The CT-C(M − 1) model with the first method as the standard method for an MTMM design with three traits and three methods. F _{i_1} (i = 2, 3, 4) denotes the ith trait factor specific to the standard method (the first method). M _k (k = 2, 3) denotes the kth method factor. There is no method factor for items x ₂₁₁, x ₃₁₁, x ₃₂₁, and x ₄₁₁, measured by the first method

Because the trait is confounded with the standard method, the corresponding items reflect both the trait and the standard method factors, and the trait and method effects are inseparable. Therefore, the consistency coefficient and the method-specificity coefficient cannot be obtained for the items belonging to the standard method. It follows that, when assessing consistency and method specificity for aggregated items, the items measured by the standard method need to be excluded. Under the assumptions for the CT-C(M − 1) model given in Eq. 4, the population reliability coefficient, consistency coefficient, and method-specificity coefficient of the summated score $\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{x_{{ijk}}}} }$ with respect to F _{i_1}— denoted respectively by $Re{l_{{{F_{{i\_1}}}}}}$, $C{O_{{{F_{{i\_1}}}}}}$, and $M{S_{{{F_{{i\_1}}}}}}$—are given by (see the Appendix for derivations)

$$ Re{l_{{{F_{{i\_1}}}}}} = \frac{{{J_i}\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }}}{{1 + ({J_i} - 1)\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }}}, $$

(5)

$$ C{O_{{{F_{{i\_1}}}}}} = \frac{{{J_i}{{\bar{\omega }}_{{{F_{{i\_1}}}}}}}}{{1 + ({J_i} - 1)\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }}}, $$

(6)

and

$$ M{S_{{{F_{{i\_1}}}}}} = \frac{{{J_i}{{\bar{\psi }}_{{{F_{{i\_1}}}}}}}}{{1 + ({J_i} - 1)\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }}}, $$

(7)

where ${J_i} = \sum\limits_{{k = 2}}^K {{J_{{ik}}}}$, $\bar{\theta }_{{{F_i}}}^{ * } = {\bar{\omega }_{{{F_{{i\_1}}}}}} + {\bar{\psi }_{{{F_{{i\_1}}}}}}$, ${\bar{\omega }_{{{F_{{i\_1}}}}}} = \frac{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2}}}{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}} + \overline {\sigma_{{{\delta_i}}}^2} }}$, ${\bar{\psi }_{{{F_{{i\_1}}}}}} = \frac{{{\Upsilon_{{{F_{{i\_1}}}}}}}}{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}} + \overline {\sigma_{{{\delta_i}}}^2} }}$, ${\Upsilon_{{{F_{{i\_1}}}}}} = \sum\limits_{{k = 2}}^K {{{\left( {{w_k}{{\bar{\lambda }}_{{{M_{{ik}}}}}}} \right)}^2} + } \sum\limits_{{k \ne k\prime }} {\left( {{w_k}{{\bar{\lambda }}_{{{M_{{ik}}}}}}} \right)\left( {{w_{{k\prime }}}{{\bar{\lambda }}_{{{M_{{ik\prime }}}}}}} \right){\rho_{{{M_k}{M_{{k\prime }}}}}}}$, ${\bar{\lambda }_{{{F_{{i\_1}}}}}} = \sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{F_{{ijk}}}}}}/} } {J_i}$, ${\bar{\lambda }_{{{M_{{ik}}}}}} = \sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{M_{{ijk}}}}}}} /{J_{{ik}}}$, $\overline {{ }\sigma_{{{\delta_i}}}^2} = \sum\limits_{{k = 1}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {\sigma_{{{\delta_{{ijk}}}}}^2} } /{J_i}$, and ${w_k} = {J_{{ik}}}/{J_i}{ }(k > 1)$. $\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }$ is an extended version of the average item reliability ${\bar{\theta }_{{{F_i}}}}$. It is a reliability index excluding the effects of scale length. $C{O_{{{F_{{i\_1}}}}}}$indicates that part of the variance of the summated score (sum of the items measured with nonstandard methods) that is due to interindividual differences on F _{i_1}. $M{S_{{{F_{{i\_1}}}}}}$, on the other hand, represents that part of the variance that is due to method-specific differences (not shared with the standard method). $Re{l_{{{F_{{i\_1}}}}}} = C{O_{{{F_{{i\_1}}}}}} + M{S_{{{F_{{i\_1}}}}}}$. A large $C{O_{{{F_{{i\_1}}}}}}$ indicates high convergent validity. A large $M{S_{{{F_{{i\_1}}}}}}$reflects high method effects and low convergent validity. Since Eq. 5 is the same as Eq. 3, the relevant properties discussed in the previous section for $re{l_{{{F_i}}}}$ apply for $Re{l_{{{F_{{i\_1}}}}}}$.

${\bar{\omega }_{{{F_{{i\_1}}}}}}$ and ${\bar{\psi }_{{{F_{{i\_1}}}}}}$, both independent of scale length, can be regarded as the average item consistency and the average item method-specificity, respectively. If ${\lambda_{{{F_{{ijk}}}}}} > {\lambda_{{{M_{{ijk}}}}}}$, then the jth item for F _{i_1} is affected more by the underlying trait factor than by the kth (nonstandard) method. If ${\bar{\omega }_{{{F_{{i\_1}}}}}} > {\bar{\psi }_{{{F_{{i\_1}}}}}}$, then the items used are affected more, on average, by the trait factor than by the nonstandard methods. In contrast, if ${\lambda_{{{M_{{ijk}}}}}} > {\lambda_{{{F_{{ijk}}}}}}$, then the influence of kth method on the item is greater than the influence of its underlying trait. ${\bar{\psi }_{{{F_{{i\_1}}}}}} > {\bar{\omega }_{{{F_{{i\_1}}}}}}$ indicates that the average method effect is greater.

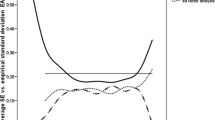
By Eq. 6, CO is no longer a fixed function of $\bar{\omega }$ and the number of items J. Since $0 \leqslant \bar{\omega } \leqslant 1$ and $0 \leqslant \bar{\psi } \leqslant 1 - \bar{\omega }$, CO is bounded below by $\bar{\omega }$ when $\bar{\psi } = 1 - \bar{\omega }$, and is bounded above by $J\bar{\omega }/(1 + (J - 1)\bar{\omega })\;( \leqslant 1)$ when $\bar{\psi } = 0$, denoted respectively by CO _L and CO _U . When $\bar{\omega } \leqslant .5$, if $\bar{\omega } \geqslant \bar{\psi }$, then $C{O_M} \leqslant CO \leqslant C{O_U}$, where $C{O_M} = J\bar{\omega }/(1 + 2(J - 1)\bar{\omega })$, occurring at $\bar{\psi } = \bar{\omega }$; otherwise $C{O_L} \leqslant CO < C{O_M}$, as marked in Fig. 2 for $\bar{\omega } = .3$ and J = 3. For any fixed value of J, CO _L , CO _U , and CO _M are all increasing functions of $\bar{\omega }$. They are pictorially presented for J = 3 through 8 in Fig. 2, using a solid line, solid curves, and dashed curves for CO _L , CO _U and CO _M , respectively. Given a value of $\bar{\omega }$, CO _U is an increasing functions of J, and, if $\bar{\omega } < .5$, CO _M is also an increasing function of J. Given values of $\bar{\omega }$ and J, the less influence the methods exert, the closer CO is to CO _U . If $\bar{\omega } \leqslant \bar{\psi }$, $\bar{\omega }$ cannot exceed .5, and $CO \leqslant C{O_M} < .5$, regardless of the value of J. Under this case, using more items while keeping the same level of $\bar{\omega }$ cannot reach any level of CO greater than .5. Given a fixed level of CO, the number of items used could be reduced by increasing $\bar{\omega }$ and further by decreasing $\bar{\psi }$. CO may be increased by eliminating the items with smaller trait loadings and larger method loadings, and/or by adding those with larger trait loadings and smaller method loadings.

Fig. 2

CO (the consistency coefficient) as a function of $\bar{\psi }$ for a given value of J and a given value of $\bar{\omega }$. $C{O_L} = \bar{\omega }$, $C{O_M} = J\bar{\omega }/(1 + 2(J - 1)\bar{\omega })$, $C{O_U} = J\bar{\omega }/(1 + (J - 1)\bar{\omega })$

By Eq. 7, MS possesses similar properties. MS is bounded below by $M{S_L} = \bar{\psi }$ when $\bar{\omega } = 1 - \bar{\psi }$, and is bounded above by $M{S_U} = J\bar{\psi }/(1 + (J - 1)\bar{\psi })\;( \leqslant 1)$ when $\bar{\omega } = 0$. When $\bar{\psi } \leqslant .5$, if $\bar{\psi } \geqslant \bar{\omega }$, then $M{S_M} \leqslant MS \leqslant M{S_U}$, where $M{S_M} = J\bar{\psi }/(1 + 2(J - 1)\bar{\psi })$, occurring at $\bar{\omega } = \bar{\psi }$; otherwise, $M{S_L} \leqslant MS < M{S_M}$. For any fixed value of J, MS _L , MS _U , and MS _M are all increasing functions of $\bar{\psi }$. They are similarly pictorially presented for J = 3 through 8 in Fig. 3. As shown in Fig. 3, given a value of $\bar{\psi }$, MS _U and MS _M are also increasing functions of J. Moreover, the less influence of the trait factor, the closer MS is to MS _U . However, MS cannot reach any level greater than .5 if $\bar{\psi } \leqslant \bar{\omega }$, regardless of the number of items used. Given a fixed level of MS, the number of items used could be reduced by increasing $\bar{\psi }$ and further by decreasing $\bar{\omega }$. The items with smaller method loadings and larger trait loadings could be considered to be eliminated to increase MS.

Fig. 3

MS (the method-specificity coefficient) as a function of $\bar{\omega }$ for a given value of J and a given value of $\bar{\psi }$. $M{S_L} = \bar{\psi }$, $M{S_M} = J\bar{\psi }/(1 + 2(J - 1)\bar{\psi })$, $M{S_U} = J\bar{\psi }/(1 + (J - 1)\bar{\psi })$

High convergent validity is not always the goal of research. Beyond the traditional search for maximum convergent validity, a thorough analysis of method influence might tell a different interesting story. Hence, a multimethod study should always have two facets: the examination of convergent validity and the analysis of method-specific influences (Eid & Diener, 2006, p. 5). When many items are selected for a trait to attain a required level of reliability, desirable convergent validity or the method effects may not be achieved with the same items. Further item selection is needed. As mentioned in Eid et al. (2003, p. 47), in personnel selection, for example, items with a low degree of method specificity and a high degree of consistency are desirable when different raters rate applicants for a position. In marital therapy, on the other hand, those items with high method specificity and low consistency are of interest if the two different raters are spouses rating each other. In this context, psychologists might be particularly interested in the divergent views of the spouses.

Empirically, since $R\hat{e}l\;\left( {{\text{the}}\;{\text{sample}}\;Rel} \right) = C\hat{O}\;\left( {{\text{the}}\;{\text{sample}}\;CO} \right) + M\hat{S}\;\left( {{\text{the}}\;{\text{sample}}\;MS} \right)$, large values of $R\hat{e}l$ may result from small values of $C\hat{O}$ (reflecting poor convergent quality) but large values of $M\hat{S}$, or from large values of $C\hat{O}$ but small values of $M\hat{S}$ (reflecting weak method influence). Acceptable reliability does not necessarily imply acceptable convergent validity or method effects. Therefore, item selection in order to improve convergent validity (or method influence) should be based on $C\hat{O}\;({\text{or}}\;M\hat{S})$ rather than on $R\hat{e}l$. Although $C\hat{O}$ can still be heightened to a required level for small $\hat{\bar{\omega }}$ (the sample $\bar{\omega }$), it works only when $\hat{\bar{\omega }} > \hat{\bar{\psi }}$ (the sample $\bar{\psi }$). A required level of $C\hat{O}$ may not be achieved if the items used are those with $\hat{\bar{\psi }} \geqslant \hat{\bar{\omega }}$. Therefore, item selection based on $C\hat{O}$ should satisfy the requirement that $\hat{\bar{\omega }} > \hat{\bar{\psi }}$. When selecting items measured by nonstandard methods, we need those with larger ${\hat{\lambda }_{{{F_j}}}}$ (the sample ${\lambda_{{{F_j}}}}$) and smaller ${\hat{\lambda }_{{{M_j}}}}$ (the sample ${\lambda_{{{M_j}}}}$) to help achieve the goal of acceptable consistency coefficient, since their inclusion can lead to a higher $\hat{\bar{\omega }}$ and a lower $\hat{\bar{\psi }}$. Similarly, item selection based on $M\hat{S}$ should satisfy the requirement that $\hat{\bar{\psi }} > \hat{\bar{\omega }}$. Eliminating an item with small ${\hat{\lambda }_{{{F_j}}}}$ and large ${\hat{\lambda }_{{{M_j}}}}$ may increase $C\hat{O}$, and eliminating an item with small ${\hat{\lambda }_{{{M_j}}}}$ and large ${\hat{\lambda }_{{{F_j}}}}$ may increase $M\hat{S}$, but the elimination may not increase $R\hat{e}l$.

An alternative approach for scale reduction

If the number of items for a trait under MTMM designs is large, item elimination would be needed to achieve parsimony. One important reason to use short scales is the reduction of being fatigued or bored resulting from answering a lengthy set of items (Lindell & Whitney, 2001; Schmitt & Stults, 1985). The properties of the consistency coefficient and the method-specificity coefficient discussed in the previous section can help assess the quality of scale items. An alternative approach for scale reduction based on $C\hat{O}\;({\text{or}}\;M\hat{S})$ and the properties discovered is proposed. Since the summated score does not include the items measured by the standard method, only those measured by nonstandard methods are considered to be eliminated.

If the goal is to enhance convergent validity, we eliminate, one at a time during the process of scale reduction, the item so that the increment of $C\hat{O}$ (denoted by $\Delta C\hat{O}$) after item elimination is maximized. We stop the process when the maximum $\Delta C\hat{O}$ becomes negative. In other words, no further elimination is allowed if convergent validity becomes worse. If the goal is to strengthen method influence, we sequentially eliminate the item for which the increment of $M\hat{S}$ (denoted by $\Delta M\hat{S}$) is maximized. We stop the elimination when the maximum $\Delta M\hat{S}$ becomes negative. The specific step-by-step procedure under the purpose of maximizing convergent validity is given as follows:

• Step 0. Compute the $C\hat{O}$ for the initial items measured by nonstandard methods.

• Step 1. Find the item whose elimination yields the maximum $C\hat{O}$ from those left in the scale. If there is only one item associated with a nonstandard method, that item is excluded from those considered to be eliminated. Update the $C\hat{O}$ and compute $\Delta C\hat{O} = {\text{new}}\;C\hat{O} - {\text{old}}\;C\hat{O}$.

• Step 2. If $\Delta C\hat{O} \geqslant 0$, then eliminate the item from the scale and then go to Step 1; otherwise, stop by returning the items left as the final choices, with the consistency coefficient of the most recently updated $C\hat{O}$.

The procedure under the purpose of maximizing method effects is similar and need not be repeated. The final reduced scale consists of the items measured by the standard method and those determined according to the procedure given above.

It is required that no nonstandard method be neglected for measuring the items in the reduced scale. Item elimination is not allowed for any trait-method unit with only one item. The trait (method) loadings of the items in the reduced scale need to be significant and $\hat{\bar{\omega }}$ needs to be greater (less) than $\hat{\bar{\psi }}$ when the purpose is to maximize convergent validity (method influence). Moreover, discriminant validity must be maintained for the reduced scale achieving the maximum of convergent validity or method effects. If any of the previously mentioned requirements is not met for the reduced scale, scale reduction fails. The proposed approach, also applicable for subscales developed for subconstructs, is recommended for scale development based on MTMM designs.

Illustration

To illustrate the approach, we use a data set generated from the model depicted in Fig. 1, in which the first method was chosen as the standard method. x ₃₁₁ and x ₃₂₁ are measured by the standard method and will not be eliminated. x ₃₁₂, x ₃₂₂, x ₃₃₂, x ₃₁₃, and x ₃₂₃ are the items measured by nonstandard methods for F ₃, which are to be further selected. The model parameters for data generation are given in Table 1 (in standard score form for ease of manipulation). They are determined based on Conway et al. (2004). The procedure given in Fan, Felsovalyi, Sivo, and Keenan (2002, Sections 4.3 and 7.2) is followed to generate a sample (N = 300) of normally distributed items, with which further item selection among x ₃₁₂, x ₃₂₂, x ₃₃₂, x ₃₁₃, and x ₃₂₃ by using the proposed approach is demonstrated. The sample correlation matrix of the items is given in Table 2.

Table 1 Population parameters of the CT-C(M − 1) model in Fig. 1 (for data generation)

Table 2 Correlation matrix of the items resulting from a data set (N = 300) generated from the CT-C(M-1) model in Fig. 1 with parameters shown in Table 1

The parameter estimates (obtained by using SAS PROC CALIS [SAS Institute Inc., 2010]) during the scale reduction process based on the CT-C(M − 1) model with M ₁ as the standard method under the purpose of maximizing convergent validity or method influence are summarized in Table 3. At each step, ${\hat{\bar{\omega }}_{{{F_{{3\_1}}}}}}$, ${\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}$, ${\hat{\Upsilon }_{{{F_{{3\_1}}}}}}$, $R\hat{e}{l_{{{F_{{3\_1}}}}}}$, and $C{\hat{O}_{{{F_{{3\_1}}}}}}$ (or $M{\hat{S}_{{{F_{{3\_1}}}}}}$) are reported for the items retained in the scale, and ${\hat{\lambda }_{{{F_{{3jk}}}}}}$ and ${\hat{\lambda }_{{{M_{{3jk}}}}}}$ are given for the item removed. It appears that model fit is adequate during the scale reduction process and parameter estimates are close to the corresponding population values, justifying our computational results.

Table 3 Parameter estimates during the process of scale reduction for F ₃ under the purpose of maximizing convergent validity or maximizing method effects based on the CT-C(M−1) model with the first method as the standard method

In the first part (when maximizing $C{\hat{O}_{{{F_{{3\_1}}}}}}$) of Table 3, ${\hat{\bar{\omega }}_{{{F_{{3\_1}}}}}}\left( { = .172} \right) < {\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}\left( { = .278} \right)$ at Step 0 for the five initial items, failing to meet the requirement and implying that $C{\hat{O}_{{{F_{{3\_1}}}}}} < C{\hat{O}_{{{F_{{3\_1}}},M}}} < .5$. It appears that some item may need to be removed. The item with the maximum increment of $C{\hat{O}_{{{F_{{3\_1}}}}}}$ after its elimination is x ₃₂₃ ($C{\hat{O}_{{{F_{{3\_1}}}}}}$ increases from .307 to .352 with $\Delta C{\hat{O}_{{{F_{{3\_1}}}}}} = .045$). Therefore, x ₃₂₃ was first eliminated. However, ${\hat{\bar{\omega }}_{{{F_{{3\_1}}}}}}\left( { = .213} \right)$ is still less than ${\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}\left( { = .259} \right)$ after excluding x ₃₂₃. Next, since x ₃₁₃ is the only item measured by M ₃ among the rest of the four items, it was compulsorily included. x ₃₃₂, with the largest $\Delta C{\hat{O}_{{{F_{{3\_1}}}}}}( = .088)$ among the rest of the three items, was subsequently removed. ${\hat{\bar{\omega }}_{{{F_{{3\_1}}}}}}\left( { = .303} \right)$, after excluding x ₃₂₃ and x _332, becomes greater than ${\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}\left( { = .229} \right)$, indicating an improvement of the average item quality. The requirement of ${\hat{\bar{\omega }}_{{{F_{{3\_1}}}}}} > {\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}$ when maximizing convergent validity has also been met. Since the elimination of any item left would worsen convergent validity, the process stopped with the final retained items of x ₃₁₂, x ₃₂₂, and x ₃₁₃, measured by nonstandard methods. $C{\hat{O}_{{{F_{{3\_1}}}}}}$ improves from .307 to .44. Although $R\hat{e}{l_{{{F_{{3\_1}}}}}}$ decreases from .804 down to .773, it should not receive concern since the purpose is to maximize convergent validity. At each step, estimates of the trait and method loadings are all highly significant (p < .01). Moreover, trait correlations show little change and all remain significantly less than 1 (p values associated with the chi-square difference tests < .001), implying that discriminant validity has been maintained while improving convergent validity by removing some “poor” items based on the consistency coefficient.

In the second part (when maximizing $M{\hat{S}_{{{F_{{3\_1}}}}}}$) of Table 3, the final items selected according to a similar procedure include x ₃₁₂, x ₃₃₂, and x ₃₂₃. x ₃₁₃ and x ₃₂₂ were sequentially removed on the basis of the criterion of achieving the largest $\Delta M{\hat{S}_{{{F_{{3\_1}}}}}}$. For the five initial items, although ${\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}\left( { = .278} \right) > {\hat{\bar{\omega }}_{{{F_{{3\_1}}}}}}\left( { = .172} \right)$; hence, $M{\hat{S}_{{{F_{{3\_1}}}}}} > M{\hat{S}_{{{F_{{3\_1}}},M}}}$, ${\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}$ is far less than .5, reflecting a need to make improvements. x ₃₁₃ was first eliminated because its elimination can lead to the maximum increase of $M{\hat{S}_{{{F_{{3\_1}}}}}}$ $\left( {\Delta M{{\hat{S}}_{{{F_{{3\_1}}}}}} = .052} \right)$. The new ${\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}\left( { = .331} \right)$ becomes greater and the difference between ${\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}$ and ${\hat{\bar{\omega }}_{{{F_{{3\_1}}}}}}\left( { = .14} \right)$ after elimination becomes bigger. The next one to be eliminated is selected from the rest of the four except x ₃₂₃ because x ₃₂₃ is the only item associated with M ₃. x ₃₂₂ was removed because its elimination results in the maximum $\Delta M{\hat{S}_{{{F_{{3\_1}}}}}}\left( { = .06} \right)$. ${\hat{\bar{\psi }}_{{{F_{{3\_1}}}}}}\left( { = .405} \right)$ becomes much greater than ${\hat{\bar{\omega }}_{{{F_{{3\_1}}}}}}\left( { = .093} \right)$ after removing x ₃₁₃ and x ₃₂₂. No further reduction was allowed. $M{\hat{S}_{{{F_{{3\_1}}}}}}$ improves from .497 to .609 whereas $R\hat{e}{l_{{{F_{{3\_1}}}}}}$ is decreasing. Again, at each step, trait loadings and method loadings are all significant, and trait correlations show little change and are all significantly less than 1 (p values < .001). Method effects have been enhanced by item elimination while maintaining discriminant validity.

The items x ₃₁₁ and x ₃₂₁ measured by the standard method are included in the final reduced scale, regardless of the purpose of maximizing convergent validity or method influence. However, the selection of the items measured by the nonstandard methods depends on the research purpose. If the purpose is to maximize convergent validity, then x ₃₁₂, x ₃₂₂, x ₃₁₃ are the choices; if the purpose is to maximize method influence, then x ₃₁₂, x ₃₃₂, x ₃₂₃ are the choices. It appears that the items selected under different purposes are somewhat different.

Discussion and conclusion

The interpretative and estimation problems that the CT–CM model suffers from can be overcome by the CT-C(M−1) model. Under the CT-C(M − 1) model, it has been shown that the reliability coefficient, the consistency coefficient, and the method-specificity coefficient of the sum of the items measured with nonstandard methods for a trait factor are all functions of the average consistency coefficient $(\bar{\omega })$, the average method-specificity coefficient $(\bar{\psi })$, and scale length. It is noteworthy that using many items for abstract trait factors may heighten convergent validity to a required level only when $\hat{\bar{\omega }} > \hat{\bar{\psi }}$, but cannot when $\hat{\bar{\omega }} \leqslant \hat{\bar{\psi }}$. In addition, given a fixed level of convergent validity, the number of items used can be reduced by increasing $\bar{\omega }$ and further by decreasing $\bar{\psi }$. A general strategy is to eliminate the items with smaller trait loadings and larger method loadings, or equivalently, to take those with larger trait loadings and smaller method loadings. If the goal is to enhance method effects, then the items with larger method loadings and smaller trait loadings should be retained.

The same principles that we have shown to find properties for CO and MS based on the CT-C(M−1) model could also be applied to the CT–CM model.

An alternative approach to reduce scale length for MTMM data based on the CT-C(M−1) model under the goal of enhancing convergent validity or method influence has been proposed. Traditional approaches for scale reduction without taking into account method factors are inappropriate for MTMM data. The items eliminated during the reduction process based on commonly used criteria in practice such as “the lowest item-total correlation” and “the largest increment of coefficient alpha” could be quite different from those determined on the basis of the criterion of the largest non-negative increment of $C\hat{O}$ (or $M\hat{S}$) proposed in this study.

If the consistency coefficient resulting from the final reduced scale is still not large enough, then the criterion of convergent validity might be released to make a compromise. If this is not possible, then it becomes necessary to return to the initial stage of scale development and reconduct item generation and item analysis. A poor item for a trait factor should be replaced by another one that can reflect the same facet of the trait domain and that can lead to a higher ${\hat{\lambda }_F}$ and a lower ${\hat{\lambda }_M}$. In the meantime, the maintenance of discriminant validity is required. Researchers should make efforts to modify existing items and/or substitute new items to achieve acceptable convergent validity, discriminant validity, and parsimony. The suggestions regarding the method-specificity coefficient are similar. Once the final scale obtained is satisfactory, it needs to be further validated by using another independent sample, as usually seen in the literature.

Note that the items retained in the final reduced scale may depend on the standard method chosen in the CT-C(M − 1) model, and the items measured by the standard method cannot be assessed because the trait factor is confounded with the standard method. It is therefore important that the choice of the standard method and the items measured by that method should be justified on the basis of theoretical considerations or consensus in the field. Following the recommendation given by Eid et al. (2003) that a “gold standard method” be chosen, we suggest that “reference items” (usually key items for the trait factor) be measured by that “gold standard method” and that other potential items be measured by nonstandard methods since item elimination is conducted only for those measured by nonstandard methods.

The multiple-item CT-C(M − 1) model, in which there are multiple items for each trait-method unit, has been given to address the problem of trait-specific method effects (Eid et al., 2003). Analyses of CO, MS, and Rel discussed in the present study can be extended for the multiple-item CT-C(M − 1) model. Statistical inference for reliability-related parameters in the model, particularly for CO and MS, needs to be further studied. In addition, how the effectiveness of the proposed approach for scale reduction is influenced by sample size is an interesting task for future research.

Appendix

Derivations of Eqs. 5, 6, and 7

By choosing the first method (k = 1) as the standard method for the CT-C(M − 1) model, the variance of the summated score $\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{x_{{ijk}}}} }$ under the assumptions for Eq. 4 and by fixing $\sigma_{{{F_{{i\_1}}}}}^2$ and $\sigma_{{{M_k}}}^2$ to 1 for identification reasons is given by

$$ \begin{array}{*{20}{c}} {Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{x_{{ijk}}}} } } \right) = Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{t_{{ijk}}}} } } \right) + Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\delta_{{ijk}}}} } } \right)} \\ { = Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{F_{{ijk}}}}}}{F_{{i\_1}}}} } } \right) + Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{M_{{ijk}}}}}}{M_k}} } } \right) + Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\delta_{{ijk}}}} } } \right)} \\ { = {{\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{F_{{ijk}}}}}}} } } \right)}^2} + \sum\limits_{{k = 2}}^K {{{\left( {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{M_{{ijk}}}}}}} } \right)}^2}} + \sum\limits_{{k \ne k\prime }} {\left( {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{M_{{ijk}}}}}}} } \right)\left( {\sum\limits_{{j = 1}}^{{{J_{{ik\prime }}}}} {{\lambda_{{{M_{{ijk\prime }}}}}}} } \right){\rho_{{_{{{M_k}{M_{{k\prime }}}}}}}}} + \sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {\sigma_{{{\delta_{{ijk}}}}}^2} } } \\ { = J_i^2{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + \sum\limits_{{k = 2}}^K {J_{{ik}}^2{{\left( {{{\bar{\lambda }}_{{{M_{{ik}}}}}}} \right)}^2} + \sum\limits_{{k \ne k\prime }} {\left( {{J_{{ik}}}{{\bar{\lambda }}_{{{M_{{ik}}}}}} \times {J_{{ik\prime }}}{{\bar{\lambda }}_{{{M_{{ik\prime }}}}}}} \right){\rho_{{_{{{M_k}{M_{{k\prime }}}}}}}}} + {J_i}\overline {\sigma_{{{\delta_i}}}^2} } } \\ { = J_i^2{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + J_i^2\sum\limits_{{k = 2}}^K {{{\left( {{w_k}{{\bar{\lambda }}_{{{M_{{ik}}}}}}} \right)}^2} + { }} J_i^2\sum\limits_{{k \ne k\prime }} {({w_k}{{\bar{\lambda }}_{{{M_{{ik}}}}}})({w_{{k\prime }}}{{\bar{\lambda }}_{{{M_{{ik\prime }}}}}}){\rho_{{_{{{M_k}{M_{{k\prime }}}}}}}}} + {J_i}\overline {\sigma_{{{\delta_i}}}^2} } \\ { = J_i^2{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + J_i^2{\Upsilon_{{{F_{{i\_1}}}}}} + {J_i}\overline {\sigma_{{{\delta_i}}}^2}, } \\ \end{array} $$

where ${J_i} = \sum\limits_{{k = 2}}^K {{J_{{ik}}}}$, ${\bar{\lambda }_{{{F_{{i\_1}}}}}} = \sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{F_{{ijk}}}}}}/{J_i}} }$ (the mean trait loading), ${\bar{\lambda }_{{{M_{{ik}}}}}} = \sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{M_{{ijk}}}}}}} /{J_{{ik}}}$ (the mean method loading for M _k ), ${\Upsilon_{{{F_{{i\_1}}}}}} = \sum\limits_{{k = 2}}^K {{{\left( {{w_k}{{\bar{\lambda }}_{{{M_{{ik}}}}}}} \right)}^2} + } \sum\limits_{{k \ne k\prime }} {\left( {{w_k}{{\bar{\lambda }}_{{{M_{{ik}}}}}}} \right)\left( {{w_{{k\prime }}}{{\bar{\lambda }}_{{{M_{{ik\prime }}}}}}} \right){\rho_{{{M_k}{M_{{k\prime }}}}}}}$, $\overline {{ }\sigma_{{{\delta_i}}}^2} = \sum\limits_{{k = 1}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {\sigma_{{{\delta_{{ijk}}}}}^2/{J_i}} }$, and ${w_k} = {J_{{ik}}}/{J_i}\;(k > 1)$. w _k represents the weight for the kth method based on the number of items associated with that method, $\sum\limits_{{k = 2}}^K {{{\left( {{w_k}{{\bar{\lambda }}_{{{M_{{ik}}}}}}} \right)}^2}}$ is the sum of squares of ${\bar{\lambda }_{{{M_{{ik}}}}}}$ weighted by w _k , and $\sum\limits_{k \ne k\prime } {\left( {{w_k}{{\bar{\lambda }}_{{M_{ik}}}}} \right)\left( {{w_{k\prime }}{{\bar{\lambda }}_{{M_{ik\prime }}}}} \right){\rho_{{M_k}{M_{k\prime }}}}}$ is the sum of products of the weighted ${\bar{\lambda }_{{{M_{{ik}}}}}}$, the weighted ${\bar{\lambda }_{{{M_{{ik\prime }}}}}}$, and their method correlations. It follows that the population reliability coefficient $Re{l_{{{F_{{i\_1}}}}}}$ of $\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{x_{{ijk}}}} }$ with respect to ${F_{{i\_1}}}$ is given by

$$ \begin{array}{*{20}{c}} {Re{l_{{{F_{{i\_1}}}}}} = \frac{{Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{t_{{ijk}}}} } } \right)}}{{Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{x_{{ijk}}}} } } \right)}}} \\ { = \frac{{J_i^2{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + J_i^2{\Upsilon_{{{F_{{i\_1}}}}}}}}{{J_i^2{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + J_i^2{\Upsilon_{{{F_{{i\_1}}}}}} + {J_i}\overline {\sigma_{{{\delta_i}}}^2} }}} \\ { = \frac{{{J_i}\left[ {{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}}} \right]}}{{({J_i} - 1)\left[ {{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}}} \right] + \left[ {{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}} + \overline {\sigma_{{{\delta_i}}}^2} } \right]}}} \\ { = \frac{{{J_i}\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }}}{{1 + ({J_i} - 1)\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }}},} \\ \end{array} $$

where $\bar{\theta }_{{{F_{{i\_1}}}}}^{ * } = \frac{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}}}}{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}} + \overline {\sigma_{{{\delta_i}}}^2} }}$. Moreover, the consistency coefficient $C{O_{{{F_{{i\_1}}}}}}$ and the method-specificity coefficient $M{S_{{{F_{{i\_1}}}}}}$ of $\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{x_{{ijk}}}} }$ with respect to ${F_{{i\_1}}}$ are given by

$$ \begin{array}{*{20}{c}} {C{O_{{{F_{{i\_1}}}}}} = \frac{{Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{F_{{ijk}}}}}}{F_{{i\_1}}}} } } \right)}}{{Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{x_{{ijk}}}} } } \right)}}} \\ { = \frac{{J_i^2{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2}}}{{J_i^2{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + J_i^2{\Upsilon_{{{F_{{i\_1}}}}}} + {J_i}\overline {\sigma_{{{\delta_i}}}^2} }}} \\ { = \frac{{{J_i}{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2}}}{{({J_i} - 1)\left[ {{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}}} \right] + \left[ {{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}} + \overline {\sigma_{{{\delta_i}}}^2} } \right]}}} \\ { = \frac{{{J_i}{{\bar{\omega }}_{{{F_{{i\_1}}}}}}}}{{1 + ({J_i} - 1)\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }}},} \\ \end{array} $$

and

$$ \begin{array}{*{20}{c}} {M{S_{{{F_{{i\_1}}}}}} = \frac{{Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{\lambda_{{{M_{{ijk}}}}}}{M_k}} } } \right)}}{{Var\left( {\sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{x_{{ijk}}}} } } \right)}}} \\ { = \frac{{J_i^2{\Upsilon_{{{F_{{i\_1}}}}}}}}{{J_i^2{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + J_i^2{\Upsilon_{{{F_{{i\_1}}}}}} + {J_i}\overline {\sigma_{{{\delta_i}}}^2} }}} \\ { = \frac{{{J_i}{\Upsilon_{{{F_{{i\_1}}}}}}}}{{({J_i} - 1)\left[ {{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}}} \right] + \left[ {{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}} + \overline {\sigma_{{{\delta_i}}}^2} } \right]}}} \\ { = \frac{{{J_i}{{\bar{\psi }}_{{{F_{{i\_1}}}}}}}}{{1 + ({J_i} - 1)\bar{\theta }_{{{F_{{i\_1}}}}}^{ * }}},} \\ \end{array} $$

where ${\bar{\omega }_{{{F_{{i\_1}}}}}} = \frac{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2}}}{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}} + \overline {\sigma_{{{\delta_i}}}^2} }}$ and ${\bar{\psi }_{{{F_i}}}} = \frac{{{\Upsilon_{{{F_{{i\_1}}}}}}}}{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {\Upsilon_{{{F_{{i\_1}}}}}} + \overline {\sigma_{{{\delta_i}}}^2} }}$. $\bar{\theta }_{{{F_{{i\_1}}}}}^{ * } = {\bar{\omega }_{{{F_{{i\_1}}}}}} + {\bar{\psi }_{{{F_{{i\_1}}}}}}$. ${\bar{\omega }_{{{F_{{i\_1}}}}}}$ and ${\bar{\psi }_{{{F_{{i\_1}}}}}}$ indicate, respectively, the average proportion of variance due to ${F_{{i\_1}}}$ and the average proportion of variance due to nonstandard methods. For the special case in which only one nonstandard method is used, we have ${\Upsilon_{{{F_{{i\_1}}}}}} = {\left( {{{\bar{\lambda }}_{{{M_{{i2}}}}}}} \right)^2}$, ${\bar{\omega }_{{{F_{{i\_1}}}}}} = \frac{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2}}}{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {{\left( {{{\bar{\lambda }}_{{{M_{{i2}}}}}}} \right)}^2} + \overline {\sigma_{{{\delta_i}}}^2} }}$, and ${\bar{\psi }_{{{F_{{i\_1}}}}}} = \frac{{{{\left( {{{\bar{\lambda }}_{{{M_{{i2}}}}}}} \right)}^2}}}{{{{\left( {{{\bar{\lambda }}_{{{F_{{i\_1}}}}}}} \right)}^2} + {{\left( {{{\bar{\lambda }}_{{{M_{{i2}}}}}}} \right)}^2} + \overline {\sigma_{{{\delta_i}}}^2} }}$.

Denoting the sample $C{O_{{{F_{{i\_1}}}}}}$, ${\bar{\omega }_{{{F_{{i\_1}}}}}}$, and ${\bar{\psi }_{{{F_{{i\_1}}}}}}$ by $C{\hat{O}_{{{F_{{i\_1}}}}}}$, ${\hat{\bar{\omega }}_{{{F_{{i\_1}}}}}}$, and ${\hat{\bar{\psi }}_{{{F_{{i\_1}}}}}}$, we have, by following Eq. 6, $C{\hat{O}_{{{F_{{i\_1}}}}}} = \frac{{{J_i}{{\hat{\bar{\omega }}}_{{{F_{{i\_1}}}}}}}}{{1 + ({J_i} - 1)\left( {{{\hat{\bar{\omega }}}_{{{F_{{i\_1}}}}}} + {{\hat{\bar{\psi }}}_{{{F_{{i\_1}}}}}}} \right)}}$, ${\hat{\bar{\omega }}_{{{F_{{i\_1}}}}}} = \frac{{{{\left( {{{\bar{\hat{\lambda }}}_{{{F_{{i\_1}}}}}}} \right)}^2}}}{{{{\left( {{{\bar{\hat{\lambda }}}_{{{F_{{i\_1}}}}}}} \right)}^2} + {{\hat{\Upsilon }}_{{{F_{{i\_1}}}}}} + \overline {\hat{\sigma }_{{{\delta_i}}}^2} }}$, ${\hat{\bar{\psi }}_{{{F_{{i\_1}}}}}} = \frac{{{{\hat{\Upsilon }}_{{{F_{{i\_1}}}}}}}}{{{{\left( {{{\bar{\hat{\lambda }}}_{{{F_{{i\_1}}}}}}} \right)}^2} + {{\hat{\Upsilon }}_{{{F_{{i\_1}}}}}} + \overline {\hat{\sigma }_{{{\delta_i}}}^2} }}$, where ${\hat{\Upsilon }_{{{F_{{i\_1}}}}}} = \sum\limits_{{k = 2}}^K {{{\left( {{w_k}{{\bar{\hat{\lambda }}}_{{{M_{{ik}}}}}}} \right)}^2}} + \sum\limits_{{k \ne k\prime }} {\left( {{w_k}{{\bar{\hat{\lambda }}}_{{{M_{{ik}}}}}}} \right)} \left( {{w_{{k\prime }}}{{\bar{\hat{\lambda }}}_{{{M_{{ik\prime }}}}}}} \right){\hat{\rho }_{{_{{{M_k}{M_{{k\prime }}}}}}}}$, ${\bar{\hat{\lambda }}_{{{F_{{i\_1}}}}}} = \sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{{\hat{\lambda }}_{{{F_{{ijk}}}}}}/{J_i}} }$, ${\bar{\hat{\lambda }}_{{{M_{{ik}}}}}} = \sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {{{\hat{\lambda }}_{{{M_{{ijk}}}}}}} /{J_{{ik}}}$, ${J_i} = \sum\limits_{{k = 2}}^K {{J_{{ik}}}}$, and $\overline {\hat{\sigma }_{{{\delta_i}}}^2} = \sum\limits_{{k = 2}}^K {\sum\limits_{{j = 1}}^{{{J_{{ik}}}}} {\hat{\sigma }_{{{\delta_{{ijk}}}}}^2} } /{J_i}$. In addition, $C{\hat{O}_{{{F_{{i\_1}}},U}}} = \frac{{{J_i}{{\hat{\bar{\omega }}}_{{{F_{{i\_1}}}}}}}}{{1 + ({J_i} - 1){{\hat{\bar{\omega }}}_{{{F_{{i\_1}}}}}}}}$, $C{\hat{O}_{{{F_{{i\_1}}},M}}} = \frac{{{J_i}{{\hat{\bar{\omega }}}_{{{F_{{i\_1}}}}}}}}{{1 + 2({J_i} - 1){{\hat{\bar{\omega }}}_{{{F_{{i\_1}}}}}}}}$, and $C{\hat{O}_{{{F_{{i\_1}}},L}}} = {\hat{\bar{\omega }}_{{{F_{{i\_1}}}}}}$. Similarly, by following Eq. 7, we have $M{\hat{S}_{{{F_{{i\_1}}}}}} = \frac{{{J_i}{{\hat{\bar{\psi }}}_{{{F_{{i\_1}}}}}}}}{{1 + \left( {{J_i} - 1} \right)\left( {{{\hat{\bar{\omega }}}_{{{F_{{i\_1}}}}}} + {{\hat{\bar{\psi }}}_{{{F_{{i\_1}}}}}}} \right)}}$. Moreover, $M{\hat{S}_{{{F_{{i\_1}}},U}}} = \frac{{{J_i}{{\hat{\bar{\psi }}}_{{{F_{{i\_1}}}}}}}}{{1 + ({J_i} - 1){{\hat{\bar{\psi }}}_{{{F_{{i\_1}}}}}}}}$, $M{\hat{S}_{{{F_{{i\_1}}},M}}} = \frac{{{J_i}{{\hat{\bar{\psi }}}_{{{F_{{i\_1}}}}}}}}{{1 + 2({J_i} - 1){{\hat{\bar{\psi }}}_{{{F_{{i\_1}}}}}}}}$, and $M{\hat{S}_{{{F_{{i\_1}}},L}}} = {\hat{\bar{\psi }}_{{{F_{{i\_1}}}}}}$.