Abstract
The interactions of sub-cycle and single-cycle pulses with two- or three-level quantum systems are studied, respectively. For the two-level quantum system, two cases in which the carrier frequency of pulses is in resonance and far from resonance with the atom are analysed. The ultrafast complete population transfer can be obtained. The sub-cycle pulse with a far off-resonant carrier frequency is found to be more suitable for the population transfer. The relation between the area of pulses and population transfer is clarified in the sub-cycle and single-cycle domain. For the Lambda-type three-level quantum system, more than 90% of population transfer can be achieved from one level to another. The scheme is insensitive to the variation of the laser parameters such as the peak Rabi frequency and the carrier frequency for both two- and three-level quantum systems.
Export citation and abstract BibTeX RIS
1. Introduction
The interaction of coherent optical pulses with quantum systems is related to many important applications [1–5]. Nowadays, with the development of laser technology, laser systems can produce controlled, intense, ultra-short optical pulses [6–14]. Various techniques have been used for pulse shaping [15]. The few-cycle pulse and sub-cycle pulses start a new era for ultrafast science. Many works have been performed on the theoretical description of single-cycle pulses, sub-cycle pulses and their interactions with matters.
The interaction of few-cycle pulses with atoms has been studied by many researchers. For example, the quantum coherent control of physical and chemical processes and also of attosecond electronic dynamics by the use of frequency- and amplitude-chirped few-cycle pulses are reported [16, 17]. In the context of coherent population transfer (CPT), the use of few-cycle laser pulses has some advantages, such as easy access to the first electronic states of many molecules and an extremely fast transfer process which can be completed on a time scale much shorter than the typical time interval between collisions of atoms or molecules [18]. The carrier envelope phase effects on the atomic excitation have been studied by the use of few-cycle pulses [19, 20].
Compared with the few-cycle laser pulse, the sub-cycle and single-cycle pulses are more suitable for the ultrafast CPT. Because of their wide frequency band, the sub-cycle and single-cycle pulses can also be used to transfer population in a multi-level system. Due to the existence of the intrinsic chirp of the sub-cycle and single-cycle pulses [21–23], the population transfer in the sub-cycle and single-cycle regimes is very different from the few-cycle and multi-cycle regimes. The population transfer of atoms by the sub-cycle and single-cycle pulses is relatively less explored and needs further investigation.
In this paper, the interactions of pulses with two- and three-level quantum systems are studied in the sub-cycle and single-cycle regimes, respectively. The expression of the sub-cycle and single-cycle pulses is described and the density matrix equations are obtained. For the two-level system, an analytical treatment of the coherent excitation is compared with the numerical treatment without the rotating-wave approximation. The relation between the area of sub-cycle or single-cycle pulses and the population transfer is clarified. The results show that the ultrafast complete CPT can be realized in a two-level system by one sub-cycle pulse. For the three-level system, more than 90% of population transfer can be obtained from one level to another by one sub-cycle laser pulse.
2. The theory of the interaction between a two-level system and the sub-cycle and single-cycle pulses
The carrier–envelope model is no longer applicable for the sub-cycle and single-cycle pulses. The dc component existing in the carrier–envelope model is found to cause nonphysical effects [21–24]. The analytical expressions of few-cycle, single-cycle and sub-cycle pulse beams with arbitrary polarization have been proposed, which are exact solutions of Maxwell's equations. For the case of a plane wave, the expression of sub-cycle and single-cycle pulses is as follows [21, 22]:
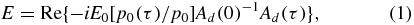
where
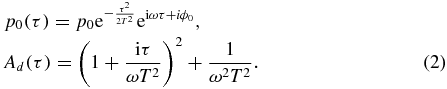
E0 is the peak value of electric field amplitude. ω is the carrier-wave frequency. T0 = 2π/ω. τ = t − t0. ϕ0 denotes the carrier–envelope phase. The temporal pulse width is defined as the full-width at half-maximum (FWHM) of the envelope function of the pulse, i.e. exp ( − τ2/(2T2)). According to equation (2), the FWHM of the pulse should be 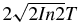 , where T is the pulse width parameter. If the pulse width is shorter than the period of oscillation of the field, T0, the pulse is referred to as a sub-cycle pulse. The peak value p0 of the dipole moment determines the peak power of the beam.
, where T is the pulse width parameter. If the pulse width is shorter than the period of oscillation of the field, T0, the pulse is referred to as a sub-cycle pulse. The peak value p0 of the dipole moment determines the peak power of the beam.
In the Schrödinger picture, we begin with the standard formulation for a two-level system driven by a classical field. Without the rotating-wave approximation, the matrix equations are given as
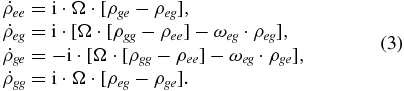
Here, Ω = μE/ℏ is the Rabi frequency and ωeg = ωe − ωg. For the sub-cycle and single-cycle pulses, the interaction time is in the fs regime. The relaxation terms in the formula are neglected.
An analytical treatment of a two-level system driven by a few-cycle pulse has been presented [25, 26]. The equations of motion for the probability amplitudes of the states |e〉 and |g〉 are given as
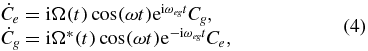
where ℏωeg is the energy difference between the states |e〉 and |g〉. Setting a function f(t) = Ce(t)/Cg(t), a Riccati equation can be obtained from equation (4):
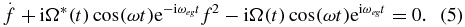
The approximate solution for equation (5), in terms of the tip angle θ for the initial condition f(τ0) = 0, is given by
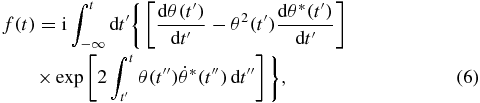
where the tip angle θ(t) is defined as
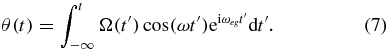
From equation (7), 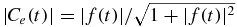 can be deduced.
can be deduced.
In figure 1, the transition frequency of the two-level quantum system is 3.0 rad fs−1 and the carrier frequency is resonant with the atom transition frequency. From figure 1(a), one can see that the numerical simulation and the analytical solution are nearly identical for a small Rabi frequency in the single-cycle regime. As shown in figure 1(b), the analytical solution is not valid for a large Rabi frequency and a large f. In this paper, the complete population transfer is studied in the sub-cycle and single-cycle regimes. The numerical simulation is chosen as the tool for the study.
Figure 1. The temporal evolution of population for the numerical solution (line) and the approximate analytical solution (dot) after applying a Gaussian single-cycle pulse. The pulse width parameter is T = 0.7 T0; 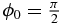 ; ω = ωeg = 3 rad fs−1. (a) The peak Rabi frequency of pulses is Ω0 = 0.5 rad fs−1. (b) The peak Rabi frequency of pulses is Ω0 = 0.8 rad fs−1.
; ω = ωeg = 3 rad fs−1. (a) The peak Rabi frequency of pulses is Ω0 = 0.5 rad fs−1. (b) The peak Rabi frequency of pulses is Ω0 = 0.8 rad fs−1.
Download figure:
Standard image High-resolution image3. Coherent population transfer of a two-level system by the sub-cycle and single-cycle pulses
In this section, the CPT of a two-level system by a sub-cycle or single-cycle pulse is investigated. Two cases in which the carrier frequency of pulses is in resonance and non-resonance with the system are analysed. The system is initially in the ground state |g〉. Equation (3) is solved numerically by a standard fourth-order Runge–Kutta method. The transition frequency of the two-level quantum system is ωeg = 3.0 rad fs−1. In figure 2, the carrier frequency of the pulse is in resonance with the system. ϕ0 = 0. In figure 2(a), 95% population transfer is obtained for the given parameters. The transition time is about 5 fs. For the sub-cycle and single-cycle pulses, the frequency chirp is the intrinsic property. From equation (1), the total phase of pulse is ![$\phi (\tau ) = \omega \tau + 2\arctan [{\mathop{\rm sgn}} (\tau )\sqrt {1 + \alpha ^2 } - \alpha ] + \phi _0 - {\pi /2}$](https://content.cld.iop.org/journals/0953-4075/46/17/175602/revision1/jpb468064ieqn4.gif) [21], where α = (1 + ω2T2 − τ2/T2)/(2ωτ). The instantaneous frequency is ωτ(τ) = dϕ(τ)/dτ. The τ-dependent frequency is highest at the centre of the pulse and blueshifted with respect to the carrier-wave frequency ω throughout the entire pulse. The relative frequency shift of instantaneous frequency versus time is shown in figure 2(c). So the population transfer in the sub-cycle regime is different from that in the few-cycle and multi-cycle regimes. Figure 2(b) shows the variation of the final population ρee(τt) with the peak Rabi frequency and the pulse width. τt is the end time of simulation. In this paper the simulation time is 40 fs. We can see that the final population transfer is fairly robust against the variation of the peak Rabi frequency. The population in the range 90–96% could be possible for the variation of Rabi frequencies in the range 1.68–3 rad fs−1. For the shorter pulses, the frequency spectrum becomes significantly broader. If the pulse width parameter T is small compared with T0, the centre frequency of the spectrum can significantly exceed the carrier frequency. So if the carrier frequency of the sub-cycle pulse is smaller than the transition frequency of the atom, it is more suitable for the population transfer.
[21], where α = (1 + ω2T2 − τ2/T2)/(2ωτ). The instantaneous frequency is ωτ(τ) = dϕ(τ)/dτ. The τ-dependent frequency is highest at the centre of the pulse and blueshifted with respect to the carrier-wave frequency ω throughout the entire pulse. The relative frequency shift of instantaneous frequency versus time is shown in figure 2(c). So the population transfer in the sub-cycle regime is different from that in the few-cycle and multi-cycle regimes. Figure 2(b) shows the variation of the final population ρee(τt) with the peak Rabi frequency and the pulse width. τt is the end time of simulation. In this paper the simulation time is 40 fs. We can see that the final population transfer is fairly robust against the variation of the peak Rabi frequency. The population in the range 90–96% could be possible for the variation of Rabi frequencies in the range 1.68–3 rad fs−1. For the shorter pulses, the frequency spectrum becomes significantly broader. If the pulse width parameter T is small compared with T0, the centre frequency of the spectrum can significantly exceed the carrier frequency. So if the carrier frequency of the sub-cycle pulse is smaller than the transition frequency of the atom, it is more suitable for the population transfer.
Figure 2. (a) The population of the excited state versus time. The pulse width parameter is T = 0.92, T0 = 1.93 fs, the peak Rabi frequency is Ω0 = 1.93 rad fs−1. (b) The population of the excited state versus the peak Rabi frequency and the pulse width parameter. (c) The relative frequency shift (Δω = ωτ − ω) as a function of time for the different pulse duration. The pulse width parameter Tvaries from 0.8 T0 to 0.3 T0.
Download figure:
Standard image High-resolution imageThe population transfer in the non-resonant case is shown in figure 3. The carrier frequency of pulses is 1 rad fs−1.
Figure 3. (a) The population of the excited state versus time when T = 0.097 T0 and Ω0 = 1.93 rad fs−1. (b) The population of the excited state versus the peak Rabi frequency and the pulse width parameter.
Download figure:
Standard image High-resolution imageIt is clear from figure 3(a) that one can obtain complete population transfer (99.9%) from the ground state |g〉 to the excited state |e〉 using one sub-cycle or single-cycle pulse. The carrier frequency of the pulse is far from resonance with the system. For the far-off resonance case, the multi-photon absorption mechanism is important for the population transfer. With a proper pulse width, the complete population transfer can be obtained. In figure 3(b), the variation of the population with the Rabi frequency and the pulse width parameter are plotted. We can see that the population transfer is sensitive to the pulse width. The population transfer could be dropped from as high as 99.9% to less than 10% when the pulse width parameter T is changed from 0.097 T0 to 0.14 T0. When the pulse is so short that the centre frequency of the spectrum covers the transition frequency, there are both one-photon and multi-photon transitions at the same time [27–29]. The rapid decrease in population can be understood as the interference between the one- and multi-photon pathways. The population transfer to the excited state |e〉 also appears sufficiently stable against the variation of the peak Rabi frequency. In fact one can obtain more than 90% population transfer for the variation of the peak Rabi frequency in the range 1.55–2.75 rad fs−1.
In figure 4, the peak Rabi frequency is chosen as 1.95 rad fs−1. One can see that the final population transfer ρee(τt) is insensitive to the variation of the carrier frequency. More than 90% population in the excited state could be possible for the variation of carrier frequency in the range 0.70–1.75 rad fs−1.
Figure 4. The population of the excited state versus the carrier frequency and the pulse width parameter. Ω0 = 1.95 rad fs−1.
Download figure:
Standard image High-resolution imageAs the high peak power of sub-cycle and single-cycle pulses is studied in this paper, the ionization of atoms needs to be investigated. Some works have been carried out about the ionization of atoms by the sub-cycle pulse [22, 30]. As shown in figures 2 and 3, perfect population transfer can be obtained when the Rabi frequency is less than the atomic transition frequency by selecting the proper peak Rabi frequency and the pulse width. For example, the complete population transfer of a two-level quantum system is obtained by a non-resonant sub-cycle pulse in figure 3. The peak Rabi frequency is 1.95 rad fs−1. The transition dipole momentum of the two-level quantum system is chosen as μ = 2.65 eÅ, which is close to the transition dipole moment existing in rubidium atoms and other atoms. The peak electric field amplitude is E0 = 4.84 × 109 V m−1. So the optical power density is P = 6.2 × 1012 w cm−2. The ionization effect can be ignored for such optical power density of a sub-cycle pulse. So by selecting the proper peak Rabi frequency and the pulse width, the ionization effect of sub-cycle pulses can be avoided and perfect population transfer can be obtained.
4. The relation between the pulse area and the population transfer
When the frequency of the driving field is in resonance with the atomic transition frequency, the population transfer in a two-level system is given by
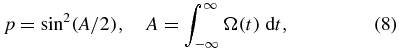
where A is the area of the pulse envelope. When A is an integer multiples of π, one can get the complete population inversion or complete population return. Formula (8) is valid for the few-cycle and multi-cycle pulses. But for the sub-cycle and single-cycle pulses, the instantaneous frequency changes with time. The relation between the area of the pulse and the population inversion in the sub-cycle and single-cycle regimes is more complicated than that in the few-cycle and multi-cycle regimes. Because of the nonphysical problem of the carrier–envelope model in the sub-cycle and single-cycle regimes [25–28], the Gaussian envelope cannot be used directly. From equation (2), one can see that the envelope of the pulse is defined as a complex envelope. The area of the sub-cycle and single-cycle pulses can be written as

where  is the envelope of the sub-cycle pulse. If we define
is the envelope of the sub-cycle pulse. If we define  and
and  ,
, 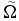 can be obtained by
can be obtained by  . The envelope
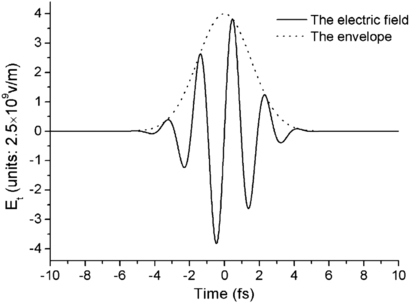
. The envelope 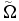 with ϕ0 = 0 is shown in figure 5. It is a single-cycle pulse with a Gaussian envelope.
with ϕ0 = 0 is shown in figure 5. It is a single-cycle pulse with a Gaussian envelope.
Figure 5. The temporal profile of the single-cycle pulse and the envelope. The pulse width parameter is T = 0.7 T0.
Download figure:
Standard image High-resolution imageAccording to the definition of the pulse width, the pulse width is 1.65 T0 in figure 5. Due to the intrinsic properties of sub-cycle and single-cycle pulses [21, 23], the amplitude of the field shows more than one oscillation in the pulse duration.
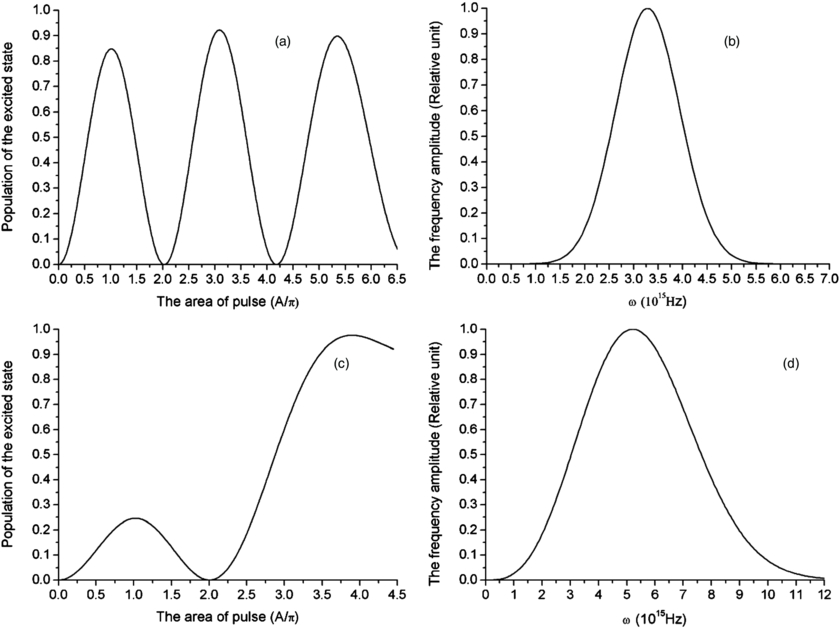
The population inversion as a function of the area of sub-cycle or single-cycle pulses is shown in figure 6. The transition frequency is 3.0 rad fs−1 and the carrier frequency is resonant with the two-level system. The area of the pulse is changed from 0 to 6.5 π in figure 6(a) and from 0 to 4.5π in figure 6(b). The system is initially in the ground state.
Figure 6. The population of the upper state versus the area of the pulse and the frequency spectrum of the pulse. The pulse width parameter T is 0.7 T0 for (a) and (b), and is 0.2 T0 for (c) and (d). The area of the pulse is 2.38 π for (b) and 0.8 π for (d).
Download figure:
Standard image High-resolution imageFigure 6 shows that the population transfer does not follow equation (8). More deviations from the equation occur for the shorter duration of the pulse. There are reports that at small pulse area the population inversion approximately coincides with the area theorem in the sub-cycle and single-cycle regimes [31, 32]. But as shown in figures 6(a) and (c), even for a small area, the curves diverge from the area theorem. The problem is that the carrier–envelope model is used for the sub-cycle and single-cycle pulses in these literatures [22, 23], where the intrinsic chirp of sub-cycle and single-cycle pulses is neglected. As shown in figures 6(c) and (d), the central frequency of the spectrum is larger than the carrier frequency. The intrinsic chirp and the centre frequency shift of the sub-cycle and single-cycle pulses are the reasons for the population deviation from the prediction of the area theorem.
5. Coherent population transfer of a three-level atom by the sub- and single-cycle pulses
Here, the coherent control of the ultrafast population transfer in a three-level Λ-type system by one sub-cycle or single-cycle pulse is considered. The three-level Λ-type system under consideration is shown in figure 7. The 1–2 transition frequency is ω1 and the 2–3 transition frequency is ω2; the transition between level |1〉 and |3〉 is electric dipole forbidden. The Hamiltonian and the evolution equations of probability amplitudes of the three-level system are written as
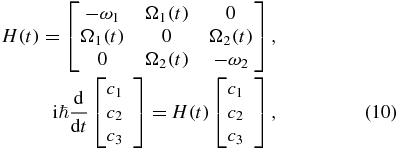
where Ω1(2)(t) = μ2, 1(3) · E(t)/ℏ is the Rabi frequency of the two transitions. For simplicity, μ12 = μ23, ω1 = 0.7 π fs−1 and ω2 = 0.8 π fs−1 are assumed.
Figure 7. Three level Λ-type system.
Download figure:
Standard image High-resolution imageThe three-level system is initially in the ground level |1〉. So that c1(τ0) = 1, We are interested in the population distribution of level |3〉 at the time τt.
It is clear from figure 8(a) that one can obtain population transfer more than 93.2% from level |1〉 to level |3〉 using one sub-cycle pulse. The transition time is about 2.5 fs. Compared with figure 8(b), we can see that the population transfer is fairly stable against the variation of the Rabi frequencies. The population transfer in the range 90.00–93.22% could be possible for the variation of peak Rabi frequencies in the range 1.22–2.20 rad fs−1. Compared with the usual scheme [4, 33], only one pulse is needed in our scheme. So the wide band of the sub-cycle and single-cycle pulses is suitable for transferring population in the multi-level system.
Figure 8. (a) Population of level |3〉 versus time. ω = 0.44 π fs−1. T = 0.2 T0. Ω0 = 1.65 rad fs−1. (b) Population of level |3〉 versus the peak Rabi frequency and the pulse width parameter. ω = 0.44 π fs−1.
Download figure:
Standard image High-resolution imageIn figure 9, the population transfer from level |1〉 to level |3〉 exhibits sufficient robustness against the variation of carrier frequency. One can obtain more than 90% population transfer for the variation of carrier frequency in the range 1.2–1.95 rad fs−1.
Figure 9. Population of level |3〉 versus the carrier frequency and the pulse width parameter. Ω0 = 1.75 rad fs−1.
Download figure:
Standard image High-resolution image6. Conclusions
The population transfer of two- and three-level quantum systems driven by the sub-cycle and single-cycle pulses has been studied. For the two-level quantum system, the numerical simulation and the analytical solution are compared and they are nearly identical for a small Rabi frequency. The atoms can be completely transferred from one level to another by one sub-cycle or single-cycle pulse. The population transfer is robust against the variation of the laser parameters such as the peak Rabi frequency and the carrier frequency. More than 90% population transfer can be obtained for the variation of the peak Rabi frequency in the range 1.55–2.75 rad fs−1 and the carrier frequency in the range 0.70–1.75 rad fs−1. The relation between the area of sub-cycle or single-cycle pulses and the population transfer is different from that of the few-cycle and multi-cycle pulses. The intrinsic chirp and the centre frequency shift of the spectrum are the reasons for the population transfer behaviour in the sub-cycle and single-cycle domain. For the Lambda-type three-level quantum system, the population transfer in the range 90.00–93.22% could be possible for the variation of peak Rabi frequencies in the range 1.22–2.20 rad fs−1 by one sub-cycle or single-cycle pulse. Due to the wide spectrum, the sub-cycle and single-cycle pulses are suitable for transferring population in the multi-level system.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (grant no 60925022), 973 Program (grant no 2013CB329501) and National Natural Science Foundation of China (grant no 11104243).