Abstract
The Folgar–Tucker fiber orientation model coupled with weakly compressible Smoothed Particle Hydrodynamics is used to simulate the process of casting of fiber reinforced concrete and to predict the spatial-temporal evolution of the probability density function of fiber orientation. The flowable concrete-fiber mix is modeled as a viscous Bingham-type fluid. Model predictions qualitatively agree with fiber orientations observed in an L-box test with fibers suspended in transparent gel. Important factors and assumptions regarding the fiber flow are reviewed and conclusions are drawn based on numerical experiments.















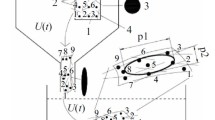
Adapted from [22]




Similar content being viewed by others
References
Advani SG, Tucker CL III (1987) The use of tensors to describe and predict fiber orientation in short fiber composites. J Rheol 31(8):751–784
Advani SG, Tucker CL III (1990) Closure approximations for three-dimensional structure tensors. J Rheol 34(3):367–386
Agboola BO, Jack DA, Montgomery-Smith S (2012) Effectiveness of recent fiber-interaction diffusion models for orientation and the part stiffness predictions in injection molded short-fiber reinforced composites. Compos Part A: Appl Sci Manuf 43(11):1959–1970
Altan MC, Subbiah S, Güçeri SI, Pipes RB (1990) Numerical prediction of three-dimensional fiber orientation in Hele–Shaw flows. Polym Eng Sci 30(14):848–859
Bay RS, Tucker CL (1992) Fiber orientation in simple injection moldings. Part I: theory and numerical methods. Polym Compos 13(4):317–331
Bay RS, Tucker CL (1992) Stereological measurement and error estimates for three-dimensional fiber orientation. Polym Eng Sci 32(4):240–253
Boulekbache B, Hamrat M, Chemrouk M, Amziane S (2010) Flowability of fibre-reinforced concrete and its effect on the mechanical properties of the material. Constr Build Mater 24(9):1664–1671
Bounoua S, Lemaire E, Férec J, Ausias G, Zubarev A, Kuzhir P (2016) Apparent yield stress in rigid fibre suspensions: the role of attractive colloidal interactions. J Fluid Mech 802:611–633
Brannon RM (2003) Functional and structured tensor analysis for engineers. New Mexico
Breitenbücher R, Meschke G, Song F, Zhan Y (2014) Experimental, analytical and numerical analysis of the pullout behaviour of steel fibres considering different fibre types, inclinations and concrete strengths. Struct Concr 15(2):126–135
Carmona S, Molins C, Aguado A, Mora F (2016) Distribution of fibers in SFRC segments for tunnel linings. Tunn Undergr Space Technol 51:238–249
Chung DH, Kwon TH (2001) Improved model of orthotropic closure approximation for flow induced fiber orientation. Polym Compos 22(5):636–649
Cintra J, Joaquim S, Tucker CL III (1995) Orthotropic closure approximations for flow-induced fiber orientation. J Rheol 39(6):1095–1122
Crespo A (2008) Development of the smoothed particle hydrodynamics model sphysics. Ph.D. thesis, Departamento de Física Aplicada. Universidad de Vigo
Crespo AJ, Domínguez JM, Rogers BD, Gómez-Gesteira M, Longshaw S, Canelas R, Vacondio R, Barreiro A, García-Feal O (2015) DualSPHysics: open-source parallel CFD solver based on smoothed particle hydrodynamics (SPH). Comput Phys Commun 187:204–216
Deeb R, Kulasegaram S, Karihaloo BL (2014) 3D modelling of the flow of self-compacting concrete with or without steel fibres. Part I: slump flow test. Comput Part Mech 1(4):373–389
Deeb R, Kulasegaram S, Karihaloo BL (2014) 3D modelling of the flow of self-compacting concrete with or without steel fibres. Part II: L-box test and the assessment of fibre reorientation during the flow. Comput Part Mech 1(4):391–408
Domínguez JM, Crespo AJ, Gómez-Gesteira M, Marongiu JC (2011) Neighbour lists in smoothed particle hydrodynamics. Int J Numer Methods Fluids 67(12):2026–2042
Fan X, Phan-Thien N, Zheng R (1998) A direct simulation of fibre suspensions. J Non-Newton Fluid Mech 74(1):113–135
Ferrara L, Cremonesi M, Faifer M, Toscani S, Sorelli L, Baril MA, Rthor J, Baby F, Toutlemonde F, Bernardi S (2017) Structural elements made with highly flowable UHPFRC: correlating computational fluid dynamics (CFD) predictions and non-destructive survey of fiber dispersion with failure modes. Eng Struct 133:141–296
Ferrara L, Ozyurt N, Di Prisco M (2011) High mechanical performance of fibre reinforced cementitious composites: the role of casting-flow induced fibre orientation. Mater Struct 44(1):109–128
Ferrara L, Shyshko S, Mechtcherine V (2012) Predicting the flow-induced dispersion and orientation of steel fibers in self-consolidating concrete by distinct element method. In: Fibre Reinforced Concrete: challenges and opportunities, Proceedings BEFIB 2012, 8th International RILEM Symposium, pp 1–12
Folgar F, Tucker CL III (1984) Orientation behavior of fibers in concentrated suspensions. J Reinf Plast Compos 3(2):98–119
Ghanbari A, Karihaloo BL (2009) Prediction of the plastic viscosity of self-compacting steel fibre reinforced concrete. Cem Concr Res 39(12):1209–1216
Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics: theory and application to non-sphericalstars. Mon Not R Astron Soc 181(3):375–389
Gomez-Gesteira M, Rogers BD, Crespo AJ, Dalrymple RA, Narayanaswamy M, Domínguez JM (2012) SPHysics-development of a free-surface fluid solver—part 1: theory and formulations. Comput Geosci 48:289–299
Grünewald S (2004) Performance-based design of self-compacting fibre reinforced concrete. Ph.D. thesis, Delft University of Technology, Department of Structural and Building Engineering
Harris J, Pittman J (1975) Equivalent ellipsoidal axis ratios of slender rod-like particles. J Colloid Interface Sci 50(2):280–282
Hérault A, Bilotta G, Vicari A, Rustico E, Del Negro C (2011) Numerical simulation of lava flow using a GPU SPH model. Annals of Geophysics 54(5):600–620
Jeffery GB (1922) The motion of ellipsoidal particles immersed in a viscous fluid. Proc R Soc Lond A: Math Phys Eng Sci 102(715):161–179
Joung C, Phan-Thien N, Fan X (2001) Direct simulation of flexible fibers. J Non-Newton Fluid Mech 99(1):1–36
Junk M, Illner R (2007) A new derivation of Jefferys equation. J Math Fluid Mech 9(4):455–488
Kang ST, Kim JK (2012) Numerical simulation of the variation of fiber orientation distribution during flow molding of ultra high performance cementitious composites (uhpcc). Cem Concr Compos 34(2):208–217
Kindlmann G (2004) Superquadric tensor glyphs. In: Proceedings of the sixth joint Eurographics—IEEE TCVG conference on visualization. Eurographics Association, pp 147–154
Kolařík F, Patzák B, Thrane L (2015) Modeling of fiber orientation in viscous fluid flow with application to self-compacting concrete. Comput Struct 154:91–100
Lucy LB (1977) A numerical approach to the testing of the fission hypothesis. Astron J 82:1013–1024
Monaghan J (2012) Smoothed particle hydrodynamics and its diverse applications. Ann Rev Fluid Mech 44:323–346
Monaghan JJ (1992) Smoothed particle hydrodynamics. Ann Rev Astron Astrophys 30(1):543–574
Monaghan JJ (2005) Smoothed particle hydrodynamics. Rep Progr Phys 68(8):1703
Montgomery-Smith S, Jack D, Smith DE (2011) The fast exact closure for Jefferys equation with diffusion. J Non-Newton Fluid Mech 166(7):343–353
Montgomery-Smith S, Jack DA, Smith DE (2010) A systematic approach to obtaining numerical solutions of Jefferys type equations using spherical harmonics. Compos Part A: Appl Sci Manuf 41(7):827–835
Morris JP, Fox PJ, Zhu Y (1997) Modeling low Reynolds number incompressible flows using SPH. J Comput Phys 136(1):214–226
Papanastasiou TC (1987) Flows of materials with yield. J Rheol 31(5):385–404
Petrie CJ (1999) The rheology of fibre suspensions. J Non-Newton Fluid Mech 87(2):369–402
Phan-Thien N, Fan XJ, Tanner R, Zheng R (2002) Folgar–Tucker constant for a fibre suspension in a Newtonian fluid. J Non-Newton Fluid Mech 103(2):251–260
Phelps JH, Tucker CL (2009) An anisotropic rotary diffusion model for fiber orientation in short-andlong-fiber thermoplastics. J Non-Newton Fluid Mech 156(3):165–176
Price DJ (2011) Smoothed particle hydrodynamics: things I wish my mother taught me. arXiv preprint arXiv:1111.1259
Sepehr M, Ausias G, Carreau PJ (2004) Rheological properties of short fiber filled polypropylene in transient shear flow. J Non-Newton Fluid Mech 123(1):19–32
Sepehr M, Carreau PJ, Moan M, Ausias G (2004) Rheological properties of short fiber model suspensions. J Rheol 48(5):1023–1048
Shao S, Lo EY (2003) Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv Water Resour 26(7):787–800
Skoptsov KA, Sheshenin SV, Galatenko VV, Malakho AP, Shornikova ON, Avdeev VV, Sadovnichy VA (2016) Particle simulation for predicting effective properties of short fiber reinforced composites. Int J Appl Mech 8(02):1650016
Stähli P, Custer R, van Mier JG (2008) On flow properties, fibre distribution, fibre orientation and flexural behaviour of FRC. Mater Struc 41(1):189–196
Vandewalle L, Heirman G, Van Rickstal F (2008) Fibre orientation in self-compacting fibre reinforced concrete. In: Proceedings of the 7th international RILEM symposium on fibre reinforced concrete: design and applications (BEFIB2008), pp 719–728
Verleye V, Couniot A, Dupret F (1993) Prediction of fiber orientation in complex injection molded parts. In: ICCM/9, vol. 3, pp. 642–650
Violeau D, Leroy A (2014) On the maximum time step in weakly compressible SPH. J Comput Phys 256:388–415
Violeau D, Rogers BD (2016) Smoothed particle hydrodynamics (SPH) for free-surface flows: past, present and future. J Hydraul Res 54(1):1–26
Švec O, Skocek J, Olesen JF, Stang H (2012) Fibre reinforced self-compacting concrete flow simulations in comparison with L-box experiments using carbopol. In: 8th Rilem international symposium on fibre reinforced concrete
Švec O, Skoček J, Stang H, Geiker MR, Roussel N (2012) Free surface flow of a suspension of rigid particles in a non-newtonian fluid: a lattice boltzmann approach. J Non-Newton Fluid Mech 179:32–42
Wang J, OGara JF, Tucker CL III (2008) An objective model for slow orientation kinetics in concentratedfiber suspensions: theory and rheological evidence. J Rheol 52(5):1179–1200
Yamane Y, Kaneda Y, Dio M (1994) Numerical simulation of semi-dilute suspensions of rodlike particlesin shear flow. J Non-Newton Fluid Mech 54:405–421
Zak G, Park C, Benhabib B (2001) Estimation of three-dimensional fibre-orientation distribution in short-fibre composites by a two-section method. J Compos Mater 35(4):316–339
Zhan Y, Meschke G (2016) Multilevel computational model for failure analysis of steel-fiber-reinforced concrete structures. J Eng Mech 142(11):04016090
Acknowledgements
Financial support was provided by the German Research Foundation (DFG) within the scope of Subprojects B2 and C4 of the Collaborative Research Centre SFB 837. This support is gratefully acknowledged. The experimental part of this work was conducted in the framework of subproject B1 of the SFB 837 by Sven Plückelmann, M.Sc., and Prof. Rolf Breitenbücher from the Chair of Building Materials at Ruhr-University Bochum, whose support is greatly appreciated.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Fitting coefficients for orthotropic closures
The coefficients for generating the orthotropic closure ORW3 according to Chung and Kwon [12] are presented below. The components \(A_{11}\), \(A_{22}\), and \(A_{33}\) are calculated according to Eq. 38.
with \(m=1,2,3\); no sum on m. Here, \(a_{1}\), \(a_{2}\), and \(a_{3}\) are eigenvalues of the second order orientation tensor, and the coefficients \({C_{m}}^{k}\) are taken according to Table 2.
Appendix B: Important matrices and vectors in Mandel notation
Formulas for the construction of Mandel vectors and Mandel matrices from 2nd and 4th order tensors are adopted here according to [9]. Note, that for symmetric tensors, due to the nature of Mandel notation, the gray entries in Eqs. 39 and 40 vanish, therefore it is sufficient to use only \(6\times 1\) and \(6\times 6\) vectors and matrices. For antisymmetric tensors, the black entries vanish.


where

and \(a_{ij}\), \(a_{ijkl}\) are components of 2nd and 4th order tensors, respectively. Reduced Strain Closure Folgar–Tucker equation for determination of the orientation state is solved for every integration point (SPH particle) at every time step.
where \({\kappa }\) is an empirical strain reduction factor (\(0\le {\kappa }\le 1\)),
with \(a_{i}\) and \({\mathbf e}_i\) being eigenvalues and eigenvectors of 2nd order orientation tensor respectively. Matrices \({\mathbf M}_1\), \({\mathbf M}_2\), \({\mathbf M}_3\) are presented below (Eqs. 44, 45, 46).



For efficient computation, the terms \(\dot{{{\varvec{\omega }}}} \cdot {\mathbf a}_2 - {\mathbf a}_2 \cdot \dot{{{\varvec{\omega }}}}\) and \(\dot{{{\varvec{\varepsilon }}}} \cdot {\mathbf a}_2 + {\mathbf a}_2 \cdot \dot{{{\varvec{\varepsilon }}}}\) on right hand side of the Eq. 41 are recast in following form:

where \(\dot{{{\omega }}}_{7}=\dot{{{\omega }}}_{\overline{32}}\), \(\dot{{{\omega }}}_{8}=\dot{{{\omega }}}_{\overline{13}}\), \(\dot{{{\omega }}}_{9}=\dot{{{\omega }}}_{\overline{21}}\).

where \(\dot{{\varepsilon }}_1=\dot{{\varepsilon }}_{11}\), \(\dot{{\varepsilon }}_2=\dot{{\varepsilon }}_{22}\), \(\dot{{\varepsilon }}_3=\dot{{\varepsilon }}_{33}\), \(\dot{{\varepsilon }}_4=\dot{{\varepsilon }}_{\underline{23}}\), \(\dot{{\varepsilon }}_5=\dot{{\varepsilon }}_{\underline{31}}\), \(\dot{{\varepsilon }}_6=\dot{{\varepsilon }}_{\underline{12}}\). Note, that \(\dot{{{\varvec{\omega }}}}\) is an antisymmetric tensor and \(\dot{{{\varvec{\varepsilon }}}}\) is symmetric and, consequently, many terms vanish due to the use of Mandel notation. The remaining terms of Eq. 41 do not need a special treatment and are just recast into Mandel notation according to Eqs. 39 and 40.
Appendix C: Rotation of fourth order tensor in Mandel notation
After the orthotropic closure tensor is generated according to Eq. 38, it needs to be rotated from principal into the initial coordinate system according to
Rotation tensor is given below (Eq. 50).

with \(e_{ij}\) being the components of three eigenvectors \({\mathbf e}_{i}\) of the second order orientation tensor.
Rights and permissions
About this article
Cite this article
Gudžulić, V., Dang, T.S. & Meschke, G. Computational modeling of fiber flow during casting of fresh concrete. Comput Mech 63, 1111–1129 (2019). https://doi.org/10.1007/s00466-018-1639-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-018-1639-9