Asymptotic inference for maximum likelihood estimators under the special exponential family with double-truncation

Abstract

Biased sampling affects the inference for population parameters of interest if the sampling mechanism is not appropriately handled. This paper considers doubly-truncated data arising in lifetime data analysis in which samples are subject to both left- and right-truncations. To correct for the sampling bias with doubly-truncated data, maximum likelihood estimator (MLE) has been proposed under a parametric family called the special exponential family (Efron and Petrosian, in J Am Stat Assoc 94:824–834, 1999). However, there is still a lack of justifying the fundamental properties for the MLE, including consistency and asymptotic normality. In this paper, we point out that the classical asymptotic theory for the independent and identically distributed data is not suitable for studying the MLE under double-truncation due to the non-identical truncation intervals. Alternatively, we formalize the asymptotic results under independent but not identically distributed data that suitably takes into account for the between-sample heterogeneity of truncation intervals. We establish the consistency and asymptotic normality of the MLE under a reasonably simple set of regularity conditions. Then, we give asymptotically valid techniques to estimate standard errors and to construct confidence intervals. Simulations are conducted to verify the suggested techniques, and childhood cancer data are used for illustration.

Appendices

Appendix 1: Proofs

1.1 Proof of Lemma 1

It suffices to check that the $k\times k$ matrix $\partial ^{2}\ell _n (\varvec{\eta })/\partial {\varvec{\eta }} ^{2}$ is negative semi-definite for any $\varvec{\upeta } \in \Theta$. Define

$$\begin{aligned} E_i^j (\varvec{\eta })=\mathop \int \limits _{R_i \cap {{\textsf {y}}}} {y^{j}\exp \{\varvec{\upeta } ^{\mathrm{T}}\cdot \mathbf{t}(y)\}dy} ,\quad j=0,1,\ldots ,3k. \end{aligned}$$

With these notations, the log-likelihood is written as

$$\begin{aligned} \ell _n (\varvec{\eta })=\sum _{i=1}^n {\varvec{\upeta } ^{\mathrm{T}}\cdot \mathbf{t}(y_i )} -\sum _{i=1}^n {\log E_i^0 (\varvec{\eta })}. \end{aligned}$$

As in Hu and Emura (2015), the score functions are

$$\begin{aligned} \frac{\partial }{\partial \eta _j }\ell _n (\varvec{\eta }) =\sum _{i=1}^n {\{y_i^j -E_i^j (\varvec{\eta })/E_i^0 (\varvec{\eta })\}} , \quad \quad j=1,2,\ldots ,k, \end{aligned}$$

and the second-order derivatives of the log-likelihood are

$$\begin{aligned} \frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\eta })= & {} -\sum _{i=1}^n [E_i^{j+s} (\varvec{\eta })/E_i^0 (\varvec{\eta })\\&-\{E_i^j (\varvec{\eta })/E_i^0 (\varvec{\eta })\}\{E_i^s (\varvec{\eta })/E_i^0 (\varvec{\eta })\}] \\= & {} -\sum _{i=1}^n {Cov_i (Y^{j},Y^{s}|\varvec{\upeta })} ,\quad j,s=1,2,\ldots ,k. \end{aligned}$$

Let $\mathbf{Cov}_i \{\mathbf{t}(Y)|\varvec{\upeta } \}$ be the covariance matrix whose (j, s) element is $Cov_i (Y^{j},Y^{s}|\varvec{\upeta })$, $j,s=1,2,\ldots ,k$. Then,

$$\begin{aligned} \frac{\partial ^{2}\ell _n (\varvec{\eta })}{\partial {\varvec{\eta }} ^{2}}=-\sum _{i=1}^n {\mathbf{Cov}_i \{\mathbf{t}(Y)|\varvec{\upeta }\}}. \end{aligned}$$

Since the covariance matrices $\mathbf{Cov}_i \{\mathbf{t}(Y)|\varvec{\upeta }\}$, $i=1,2,\ldots ,n$ are positive semi-definite (see p. 287, Theorem B.2 of Sen and Srivastava 1990), their sum is also positive semi-definite. Hence, $\partial ^{2}\ell _n (\varvec{\eta })/\partial {\varvec{\eta }} ^{2}$ is negative semi-definite. $\square$

1.2 Proof of Theorem 1 (a): Existence and consistency

Under Assumption (A), one can define a subset of $\Theta$,

$$\begin{aligned} Q_a =\{\varvec{\upeta } =(\eta _1 ,\eta _2 ,\ldots ,\eta _k){:}||\varvec{\upeta } -\varvec{\upeta } ^{0}||^{2}\le a^{2}\}, \end{aligned}$$

where $||\varvec{\upeta } ||^{2}=\varvec{\upeta } ^{\mathrm {T}}\varvec{\upeta }$ and $a>0$ is a small number, which produces a sphere with center $\varvec{\upeta } ^{0}$ and radius a.The surface of $Q_a$ is defined as

$$\begin{aligned} \partial Q_a =\{\varvec{\upeta } =(\eta _1 ,\eta _2 ,\ldots ,\eta _k){:}||\varvec{\upeta } -\varvec{\upeta } ^{0}||^{2}=a^{2}\}. \end{aligned}$$

Now, we will show that for any sufficiently small a and for any $\varvec{\upeta } \in \partial Q_a$,

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\{\ell _n (\varvec{\upeta })<\ell _n (\varvec{\upeta } ^{0})\}=\mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ {\frac{1}{n}\ell _n (\varvec{\upeta })-\frac{1}{n}\ell _n (\varvec{\upeta } ^{0})<0} \right\} =1. \end{aligned}$$

This implies that, with probability tending to one, there exists a local maxima in $Q_a$, which solves Eq. (4).

By a Taylor expansion, we expand the log-likelihood about the true value $\varvec{\upeta } ^{0}$ as

$$\begin{aligned} \begin{aligned} \ell _n (\varvec{\upeta })&=\ell _n (\varvec{\upeta } ^{0})+\sum _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }} \right\} (\eta _j -\eta _j^0 )} \\&\quad +\frac{1}{2!}\sum _{j=1}^k {\sum _{s=1}^k {\left\{ {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta } \Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }} \right\} (\eta _j -\eta _j^0)} } (\eta _s -\eta _s^0) \\&\quad +\frac{1}{3!}\sum _{j=1}^k \sum _{s=1}^k \sum _{l=1}^k \left\{ {\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l } {\ell _n (\varvec{\upeta })} \Bigg |_{\varvec{\upeta } =\varvec{\upeta } ^{*}} } \right\} \\&\quad \times (\eta _j -\eta _j^0) (\eta _s -\eta _s^0) (\eta _l -\eta _l^0), \end{aligned} \end{aligned}$$

(6)

where $\varvec{\upeta } ^{*}$ is on the line between $\varvec{\upeta }$ and $\varvec{\upeta } ^{0}$. By Assumption (C), there is a measurable function $M_{jsl}$ such that

$$\begin{aligned} -M_{jsl} (y)\le \frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\log f_i (y|\varvec{\upeta } ^{*})\le M_{jsl} (y),\quad i=1,2,\ldots ,n. \end{aligned}$$

This implies that

$$\begin{aligned} \frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\log f_i (y|\varvec{\upeta } ^{*})=\gamma _{jsl} (y|\varvec{\upeta } ^{*})\cdot M_{jsl} (y), \end{aligned}$$

for some $\gamma _{jsl} (y|\varvec{\upeta } ^{*})\in [-1,1]$. Thus

$$\begin{aligned} \frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\left. {\ell _n (\varvec{\upeta } )} \right| _{\varvec{\upeta } =\varvec{\upeta } ^{*}} =\sum _{i=1}^n {\gamma _{jsl} (y_i |\varvec{\upeta } ^{*})} \cdot M_{jsl} (y_i). \end{aligned}$$

Then, we rewrite Eq. (6) to yield

$$\begin{aligned} \frac{1}{n}\ell _n (\varvec{\upeta } )- \frac{1}{n}\ell _n (\varvec{\upeta } ^{0})= & {} \frac{1}{n}\sum _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta } )\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }} \right\} (\eta _j -\eta _j^0 )} \\&+\frac{1}{2n}\sum _{j=1}^k {\sum _{s=1}^k {\left\{ {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta } )\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }} \right\} (\eta _j -\eta _j^0 )} } (\eta _s -\eta _s^0 ) \\&+\frac{1}{6n}\sum _{j=1}^k {\sum _{s=1}^k {\sum _{l=1}^k {(\eta _j -\eta _j^0 )} } (\eta _s -\eta _s^0)(\eta _l -\eta _l^0 )} \sum _{i=1}^n {\gamma _{jsl} (y_i |\varvec{\upeta } ^{*})} \cdot M_{jsl} (y_i) \\\equiv & {} S_{n,1} (\varvec{\upeta })+S_{n,2} (\varvec{\upeta })+S_{n,3} (\varvec{\upeta }). \\ \end{aligned}$$

Here, we define

$$\begin{aligned} \left\{ \begin{array}{l} {S_{n,1} (\varvec{\upeta })\equiv \frac{1}{n}\mathop \sum \limits _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}} \right\} (\eta _j -\eta _j^0 )},} \\ {S_{n,2} (\varvec{\upeta })\equiv \frac{1}{2n}\mathop \sum \limits _{j=1}^k {\mathop \sum \limits _{s=1}^k {\left\{ {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg |{_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }} \right\} (\eta _j -\eta _j^0)} } (\eta _s -\eta _s^0),} \\ {S_{n,3} (\varvec{\upeta })\equiv \frac{1}{6n}\mathop \sum \limits _{j=1}^k {\mathop \sum \limits _{s=1}^k {\mathop \sum \limits _{l=1}^k {(\eta _j -\eta _j^0 )} } (\eta _s -\eta _s^0) (\eta _l -\eta _l^0)} \mathop \sum \limits _{i=1}^n {\gamma _{jsl} (y_i |\varvec{\upeta } ^{*})} \cdot M_{jsl} (y_i).} \\ \end{array} \right. \end{aligned}$$

Our target is to prove that, for a sufficiently small a and for any $\varvec{\upeta } \in \partial Q_a$,

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P \left\{ {\frac{1}{n}\ell _n (\varvec{\upeta })- \frac{1}{n}\ell _n (\varvec{\upeta } ^{0})<0} \right\} =\mathop {\lim }\limits _{n\rightarrow \infty } P\{S_{n,1} (\varvec{\upeta })+S_{n,2} (\varvec{\upeta })+S_{n,3} (\varvec{\upeta } ) < 0 \}=1. \end{aligned}$$

By Lemma 2 (WLLN) and Assumption (B), one can obtain

$$\begin{aligned} \frac{1}{n}\frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }=\frac{1}{n}\sum _{i=1}^n {\frac{\partial }{\partial \eta _j }\log f_i (Y_i |\varvec{\upeta } )\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} } \mathop {\longrightarrow }\limits ^{p}0} , \end{aligned}$$

(7)

where we have verified the condition of Lemma 2 with $p=2$ by

$$\begin{aligned}&\mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n^{2}}\sum _{i=1}^n {E\left\{ {\frac{\partial }{\partial \eta _j }\log f_i (Y_i |\varvec{\upeta } ^{0})} \right\} ^{2}} \\&\quad =\mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n}\cdot \frac{1}{n}\sum _{i=1}^n {E\left\{ {\frac{\partial }{\partial \eta _j }\log f_i (Y_i |\varvec{\upeta } ^{0})} \right\} ^{2}} =\mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n}I_{jj} (\varvec{\upeta } ^{0})=0. \end{aligned}$$

Note that

$$\begin{aligned} \frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s } \ell _n (\varvec{\upeta } ) \Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }= & {} \frac{1}{n}\sum _{i=1}^n {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }} \log f_i (y_i |\varvec{\upeta } )\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}} \nonumber \\= & {} \frac{1}{n}\sum _{i=1}^n {\left[ {\left\{ {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\log f_i (y_i |\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}} \right\} -\{-I_{i,js} (\varvec{\upeta } ^{0})\}} \right] }\qquad \\&-\frac{1}{n}\sum _{i=1}^n {I_{i,js} (\varvec{\upeta } ^{0})}.\nonumber \end{aligned}$$

(8)

By Lemma 2 and Assumptions (B) and (D), Eq. (8) converges in probability to $-I_{js} (\varvec{\upeta } ^{0})$, where we have verified the condition of Lemma 2 with $p=2$ by

$$\begin{aligned}&\mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n^{2}} \sum _{i=1}^n {E\left\{ {\left. {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\log f_i (Y_i |\varvec{\upeta } )} \right| _{\varvec{\upeta } =\varvec{\upeta } ^{0}}} \right\} ^{2}} \le \mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n}\cdot \frac{1}{n}\sum _{i=1}^n {w_{i,js}^2 } \\&\quad =\mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n}\cdot w_{js}^2 =0. \end{aligned}$$

Step 1 $\mathop {\lim }\limits _{n\rightarrow \infty } P\{|S_{n,1} (\varvec{\upeta })|<ka^{3}\}=1$ for any $\varvec{\upeta } \in \partial Q_a$:

Since $|\eta _j -\eta _j^0 |\le a$ for any $\varvec{\upeta } \in \partial Q_a$, we have

$$\begin{aligned} |S_{n,1} (\varvec{\upeta } )|\le a\sum _{j=1}^k {\left| {\frac{1}{n}\frac{\partial }{\partial \eta _j }\ell _n (\varvec{\eta })|_{\varvec{\upeta } =\varvec{\upeta } ^{0}} } \right| }. \end{aligned}$$

This implies

$$\begin{aligned} \{|S_{n,1} (\varvec{\upeta } )|<ka^{3}\}\supset \left\{ {a\sum _{j=1}^k {\left| {\frac{1}{n}\frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta } )\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} } } \right| } <ka^{3}} \right\} . \end{aligned}$$

Thus, we have

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\{|S_{n,1} (\varvec{\upeta } )|<ka^{3}\}\ge \mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ {a\sum _{j=1}^k {\left| {\frac{1}{n}\frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} } } \right| } <ka^{3}} \right\} =1, \end{aligned}$$

where the last equation follows from Eq. (7).

Step 2 $\mathop {\lim }\limits _{n\rightarrow \infty } P\{S_{n,2} (\varvec{\upeta })<-ca^{2}\}=1$ for some $c>0$ and for any $\varvec{\upeta } \in \partial Q_a$:

$$\begin{aligned} \begin{aligned} 2S_{n,2} (\varvec{\upeta })=&\frac{1}{n}\sum _{j=1}^k {\sum _{s=1}^k {\left\{ {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}} \right\} (\eta _j -\eta _j^0)(\eta _s -\eta _s^0)} } \\ =&\sum _{j=1}^k {\sum _{s=1}^k {\left[ {\frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} } - \{-I_{js} (\varvec{\upeta } ^{0})\}} \right] (\eta _j -\eta _j^0)(\eta _s -\eta _s^0)} }\\&-\sum _{j=1}^k {\sum _{s=1}^k {I_{js} (\varvec{\upeta } ^{0})(\eta _j -\eta _j^0)(\eta _s -\eta _s^0)} } \\ \equiv&B_n (\varvec{\upeta })+B(\varvec{\upeta }), \end{aligned} \end{aligned}$$

(9)

where we define

$$\begin{aligned} B_n (\varvec{\upeta })\equiv & {} \sum _{j=1}^k {\sum _{s=1}^k {\left[ {\frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}} - \{-I_{js} (\varvec{\upeta } ^{0})\}} \right] (\eta _j -\eta _j^0)(\eta _s -\eta _s^0)} } , \\ B(\varvec{\upeta })\equiv & {} \sum _{j=1}^k {\sum _{s=1}^k {\{-I_{js} (\varvec{\upeta } ^{0})\}(\eta _j -\eta _j^0)(\eta _s -\eta _s^0 )} }. \end{aligned}$$

For $\varvec{\upeta } \in \partial Q_a$, we know that $|\eta _j -\eta _j^0 |\le a$ and $|\eta _s -\eta _s^0 |\le a$. Thus

$$\begin{aligned} |B_n (\varvec{\upeta })|\le a^{2}\sum _{k=1}^k {\sum _{s=1}^k {\left| {\frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} } -\{-I_{js} (\varvec{\upeta } ^{0})\}} \right| } }. \end{aligned}$$

By arguments following Eq. (8),

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\left( {\left| {\frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }-\{-I_{js} (\varvec{\upeta } ^{0})\}} \right| <\varepsilon } \right) =1, \end{aligned}$$

for $\varepsilon >0$. $\hbox {Letting }\varepsilon =a,$

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\left( {\sum _{j=1}^k {\sum _{s=1}^k {a^{2}\left| {\frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}} - \{-I_{js} (\varvec{\upeta } ^{0})\}} \right| <k^{2}a^{3}} } } \right) =1. \end{aligned}$$

(10)

Note that

$$\begin{aligned} B(\varvec{\upeta })= & {} \sum _{j=1}^k {\sum _{s=1}^k {\{-I_{js} (\varvec{\upeta } ^{0})\}} } (\eta _j -\eta _j^0)(\eta _s -\eta _s^0)=(\varvec{\upeta } -\varvec{\upeta } ^{0})^{\mathrm {T}}\{-I(\varvec{\upeta } ^{0})\}(\varvec{\upeta } -\varvec{\upeta } ^{0}) \\= & {} (\varvec{\upeta } -\varvec{\upeta } ^{0})^{\mathrm {T}}\{\Gamma \Lambda \Gamma ^{\mathrm {T}}\}(\varvec{\upeta } -\varvec{\upeta } ^{0})=\{\Gamma ^{\mathrm {T}}(\varvec{\upeta } -\varvec{\upeta } ^{0})\}^{\mathrm {T}}\cdot \Lambda \cdot \Gamma ^{\mathrm {T}}(\varvec{\upeta } -\varvec{\upeta } ^{0}), \end{aligned}$$

where $\Lambda =diag(\lambda _1, \lambda _2 ,\ldots , \lambda _k )$ is a diagonal matrix of the eigenvalues of $-I(\varvec{\upeta } ^{0})$ and $\Gamma$ is a orthogonal matrix ($\Gamma \Gamma ^{\mathrm {T}}=\hbox {I})$ whose column i corresponds to the eigenvector of $\lambda _i$. We order the eigenvalues such that $\lambda _k \le \cdots \le \lambda _2 \le \lambda _1$ and arrange $\Gamma$ accordingly. By Assumption (B), we know that $\lambda _1 <0$. Letting ${\varvec{\xi }} =\Gamma ^{\mathrm {T}}(\varvec{\upeta } -\varvec{\upeta } ^{0})$,

$$\begin{aligned} B(\varvec{\upeta })=\mathop \sum \nolimits _{i=1}^k {\lambda _i \xi _i^2 } \le \mathop \sum \nolimits _{i=1}^k {\lambda _1 \xi _i^2 } =\lambda _1 {\varvec{\xi }} ^{\mathrm {T}}{\varvec{\xi }} =\lambda _1 (\varvec{\upeta } -\varvec{\upeta } ^{0})^{\mathrm {T}}(\varvec{\upeta } -\varvec{\upeta } ^{0})=\lambda _1 a^{2}.\nonumber \\ \end{aligned}$$

(11)

Form Eq. (10), we have

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P(|B_n (\varvec{\upeta })|<k^{2}a^{3})=\mathop {\lim }\limits _{n\rightarrow \infty } P(B_n (\varvec{\upeta } )<k^{2}a^{3})=1, \end{aligned}$$

and from Eq. (11), we know $B(\varvec{\upeta } )\le \lambda _1 a^{2}$. Thus,

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ {S_{n,2} (\varvec{\upeta })<\frac{k^{2}}{2}a^{3}+\frac{\lambda _1 }{2}a^{2}} \right\} =1. \end{aligned}$$

There always exist constants $c_0 >0$ and $a_0 >0$ such that, for $a<a_0$ and $0<c<c_0$,

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\{S_{n,2} (\varvec{\upeta })<-ca^{2}\}=1. \end{aligned}$$

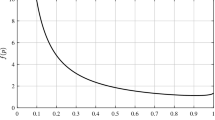
The idea of choosing $c_0$ and $a_0$ is conveniently explained under $k=3$ as follows: We wish to find a range of a such that $9a^{3}/2+\lambda _1 a^{2}/2\le -ca^{2}$. This is explained in Fig. 3. Concretely,

$$\begin{aligned} f(a)=\frac{9}{2}a^{3}+\frac{\lambda _1 }{2}a^{2}\Rightarrow & {} {f}'(a)=\frac{27}{2}a^{2}+\lambda _1 a=0\quad \Rightarrow \quad a=\frac{-2\lambda _1 }{27} \\\Rightarrow & {} {f}''(a)=27a+\lambda _1 |_{a=-2\lambda _1 /27} =-\lambda _1 >0. \end{aligned}$$

Then, f(a) has the local minimum at $a_0 =-2\lambda _1 /27>0$, and $c_0$ can be obtained by solving

$$\begin{aligned} \frac{9a^{3}}{2}+\frac{\lambda _1 a^{2}}{2}=-ca^{2}\Rightarrow c=-\frac{\lambda _1 }{2}-\frac{9a}{2}. \end{aligned}$$

Hence, $c_0 =-\lambda _1 /2-9a_0 /2=-\lambda _1 /6>0$ as seen in Fig. 3.

The values $a_0$ and c are chosen such that $f(a)\le g(a)$ for all $a<a_0$.

Step 3 $\mathop {\lim }\limits _{n\rightarrow \infty } P\{|S_{n,3} (\varvec{\upeta })|<ba^{3}\}=1$ for some $b>0$ and for any $\varvec{\upeta } \in \partial Q_a$:

Fig. 3

The sketch of $f(a)=9a^{3}/2+\lambda _1 a^{2}/2$ and $g(a)=-ca^{2}$

By Lemma 2 and Assumption (C), we obtain

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n {M_{jsl} (Y_i)}= & {} \frac{1}{n}\sum _{i=1}^n {[M_{jsl} (Y_i)} -E\{M_{jsl} (Y_i )\}]\\&+\frac{1}{n}\sum _{i=1}^n {E\{M_{jsl} (Y_i )\}} \mathop {\longrightarrow }\limits ^{p}m_{jsl} , \end{aligned}$$

where we have verified the condition $p=2$ of Lemma 2 by

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n^{2}} \sum _{i=1}^n {E[M_{jsl} (Y_i )^{2}]} =\mathop {\lim } \limits _{n\rightarrow \infty } \frac{1}{n}\frac{1}{n}\sum _{i=1}^n {E[M_{jsl} (Y_i )^{2}]}=\mathop {\lim }\limits _{n\rightarrow \infty } \frac{1}{n}\frac{1}{n}\sum _{i=1}^n {m_{i,jsl}^2 } =0. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ \left| \frac{1}{n}\sum _{i=1}^n M_{jsl} (Y_i )-m_{jsl} \right| <\varepsilon \right\} =1. \end{aligned}$$

Letting $\varepsilon =m_{jsl}$ and by $M_{jsl} (Y_i )>0$,

$$\begin{aligned} \begin{aligned}&\mathop {\lim }\limits _{n\rightarrow \infty } P \left\{ \left| \frac{1}{n}\sum _{i=1}^n M_{jsl} (Y_i )-m_{jsl} \right| <m_{jsl} \right\} \\&\quad =\mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ {\frac{1}{n}\sum _{i=1}^n {M_{jsl} (Y_i )<2m_{jsl} } } \right\} =1. \end{aligned} \end{aligned}$$

(12)

When $\varvec{\upeta } \in \partial Q_a$, we have $|\eta _j -\eta _j^0 |$, $|\eta _s -\eta _s^0 |$, $|\eta _l -\eta _l^0 |\le a$. Thus,

$$\begin{aligned} |S_{n,3} (\varvec{\upeta })|\le & {} \frac{a^{3}}{6} \sum _{j=1}^k {\sum _{s=1}^k {\sum _{l=1}^k {\left| {\frac{1}{n}\sum _{i=1}^n {\gamma _{jsl} (y_i |\varvec{\upeta } ^{*})} M_{jsl} (y_i )} \right| } } }\\\le & {} \frac{a^{3}}{6}\sum _{j=1}^k {\sum _{s=1}^k {\sum _{l=1}^k {\frac{1}{n}\sum _{i=1}^n {M_{jsl} (y_i )} } } }. \end{aligned}$$

For any given $a>0$, it follows from (12) that

$$\begin{aligned} 1= & {} \mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ {\frac{a^{3}}{6}\sum _{j=1}^k {\sum _{s=1}^k {\sum _{l=1}^k {\frac{1}{n}\sum _{i=1}^n {M_{jsl} (Y_i )} } } } <\frac{a^{3}}{6}\sum _{j=1}^k {\sum _{s=1}^k {\sum _{l=1}^k {2m_{jsl} } } } } \right\} \\= & {} \mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ {\frac{a^{3}}{6}\sum _{j=1}^k {\sum _{s=1}^k {\sum _{l=1}^k {\frac{1}{n}\sum _{i=1}^n {M_{jsl} (Y_i )} } } } <\frac{a^{3}}{3}\sum _{j=1}^k {\sum _{s=1}^k {\sum _{l=1}^k {m_{jsl} } } } } \right\} . \end{aligned}$$

This implies the desired result

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\{|S_{n,3} (\varvec{\upeta })|<ba^{3}\}=1, \quad b=\frac{1}{3}\sum _{j=1}^k {\sum _{s=1}^k {\sum _{l=1}^k {m_{jsl} } } }. \end{aligned}$$

Combining the results of Steps 1–3, we know that

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ S_{n,1} (\varvec{\upeta })+S_{n,2} (\varvec{\upeta })+S_{n,3} (\varvec{\upeta } )<ka^{3}-ca^{2}+ba^{3}\right\} =1, \end{aligned}$$

and that

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P\left\{ {\frac{1}{n}\ell _n (\varvec{\upeta })-\frac{1}{n}\ell _n (\varvec{\upeta } ^{0})<ka^{3}-ca^{2}+ba^{3}} \right\} =1. \end{aligned}$$

To complete the proof, we choose a such that $ka^{3}-ca^{2}+ba^{3}<0$, equivalently $a<c/(b+k)$. This is possible by taking a as small as possible. With this choice, there always exists ${\hat{\varvec{\upeta }}}_n$ such that $\{\ell _n (\varvec{\upeta })-\ell _n (\varvec{\upeta } ^{0})<0\}\subset \{||{\hat{\varvec{\upeta }}}_n -\varvec{\upeta } ^{0}||\le a\}$ with probability tending to one. Please see Fig. 4 for our numerical example of $k=3$ in which the preceding relationship occurs. Therefore, letting $\varepsilon =a$, we have shown the existence of ${\hat{\varvec{\upeta }}}_n$ (with probability tending to one) and consistency simultaneously as

$$\begin{aligned} \mathop {\lim }\limits _{n\rightarrow \infty } P(||{\hat{\varvec{\upeta }}}_n -\varvec{\upeta } ||\le \varepsilon )\ge \mathop {\lim }\limits _{n\rightarrow \infty } P(\ell _n (\varvec{\upeta })-\ell _n (\varvec{\upeta } ^{0})<0)=1. \end{aligned}$$

Fig. 4

The occurrence $\{\ell _n (\varvec{\upeta })-\ell _n (\varvec{\upeta } ^{0})<0\}\subset \{||{\hat{\varvec{\upeta }}}_n -\varvec{\upeta } ^{0}||\le a\}$, where $\varvec{\upeta } ^{0}=(\eta _1^0 ,\eta _2^0, \eta _3^0)$ and $\varvec{\upeta } \in \partial Q_a$ for a small $a>0$

1.3 Proofs of Theorem 1 (b)

By a Taylor expansion, we expand the first order derivative of log-likelihood function between the MLE ${\hat{\varvec{\upeta }}}_n$ and the true value $\varvec{\upeta } ^{0}$ as

$$\begin{aligned} 0= & {} \frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}} + \sum _{s=1}^k {\left\{ {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}} \right\} } (\hat{{\eta }}_{sn} -\eta _s^0) \\&+\frac{1}{2}\sum _{s=1}^k {\sum _{l=1}^k {\left\{ {\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } ={\tilde{\varvec{\upeta }}}_n } }} \right\} } } (\hat{{\eta }}_{sn} -\eta _s^0)(\hat{{\eta }}_{ln} -\eta _l^0), \end{aligned}$$

where ${\tilde{\varvec{\upeta }}}_n$ is on the line between ${\hat{\varvec{\upeta }}}_n$ and $\varvec{\upeta } ^{0}$. It follows that

$$\begin{aligned} \frac{\partial }{\partial \eta _j }\left. {\ell _n (\varvec{\upeta } ^{0})} \right| _{\varvec{\upeta } = \varvec{\upeta } ^{0}}= & {} -\sum _{s=1}^k {\left\{ {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }} \right\} } (\hat{{\eta }}_{sn} -\eta _s^0) \\&-\frac{1}{2}\sum _{s=1}^k {\sum _{l=1}^k {\left\{ {\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } ={\tilde{\varvec{\upeta }}}_n}}} \right\} } } (\hat{{\eta }}_{sn} -\eta _s^0)(\hat{{\eta }}_{ln} -\eta _l^0). \end{aligned}$$

Multiplying $1/\sqrt{n}$ both sides,

$$\begin{aligned} \frac{1}{\sqrt{n}}\frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta })\Bigg |{_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}= & {} \sum _{s=1}^k \left[ -\frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta } ) \Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} } \right. \\&\left. -\frac{1}{2n}\sum _{l=1}^k {\left\{ {\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l } \ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } = {\tilde{\varvec{\upeta }}}_n }}} \right\} (\hat{{\eta }}_{ln} -\eta _l^0)} \right] \\&\times \sqrt{n}(\hat{{\eta }}_{sn} -\eta _s^0). \end{aligned}$$

This is written as

$$\begin{aligned} T_{n,j} (\varvec{\upeta } ^{0})=\sum _{s=1}^k {R_{n,js} (\varvec{\upeta } ^{0})\cdot C_{n,s} } (\varvec{\upeta } ^{0}),\quad j=1,2,\ldots , k, \end{aligned}$$

where

$$\begin{aligned} T_{n,j} (\varvec{\upeta } ^{0})\equiv & {} \frac{1}{\sqrt{n}} \frac{\partial }{\partial \eta _j }\ell _n (\varvec{\upeta }) \Bigg |{_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}\\= & {} \frac{1}{\sqrt{n}}\sum _{i=1}^n {\frac{\partial }{\partial \eta _j }\log f_i (y_i |\varvec{\upeta } )\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }} , \\ R_{n,js} (\varvec{\upeta } ^{0})\equiv & {} - \frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s } \ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } = \varvec{\upeta } ^{0}}}\\&-\frac{1}{2n}\sum _{l=1}^k {\left\{ {\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\ell _n (\varvec{\upeta }) \Bigg | {_{\varvec{\upeta } ={\tilde{\varvec{\upeta }}}_n }}} \right\} (\hat{{\eta }}_{ln} -\eta _l^0)} , \\ C_{n,s} (\varvec{\upeta } ^{0})\equiv & {} \sqrt{n}(\hat{{\eta }}_{sn} -\eta _s^0). \\ \end{aligned}$$

Our target is to prove the convergence of $\mathbf{C}_n =(C_{n,1},C_{n,2} ,\ldots , C_{n,k})^{\mathrm {T}}$.

Step 1 $\mathbf{T}_n (\varvec{\upeta } ^{0})=(T_{n,1} (\varvec{\upeta } ^{0}),T_{n,2} (\varvec{\upeta } ^{0}),\ldots , T_{n,k} (\varvec{\upeta } ^{0}))^{\mathrm {T}}\mathop {\longrightarrow }\limits ^{d}N_k (\mathbf{0},I(\varvec{\upeta } ^{0}))$.

Let $\mathbf{T}_n (\varvec{\upeta } ^{0})=\sum _{i=1}^n {\mathbf{D}_{n,i}}$, where

$$\begin{aligned} \mathbf{D}_{n,i} =\left[ \begin{array}{cccc} {\frac{1}{\sqrt{n}}\frac{\partial }{\partial \eta _1 }\log f_i (y_i |\varvec{\upeta } ),}&{} {\frac{1}{\sqrt{n}}\frac{\partial }{\partial \eta _2 }\log f_i (y_i |\varvec{\upeta } ),\ldots ,}&{} {\frac{1}{\sqrt{n}}\frac{\partial }{\partial \eta _k }\log f_i (y_i |\varvec{\upeta } )} \\ \end{array} \right] ^{\mathrm {T}} \Bigg |{_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}. \end{aligned}$$

For the Lindeberg–Feller multivariate CLT to be applied, we check the Lindeberg condition in Eq. (5). For any $\varepsilon >0$,

$$\begin{aligned}&\sum _{i=1}^n {E_{\varvec{\upeta } ^{0}}(||\mathbf{D}_{n,i} -E[\mathbf{D}_{n,i} ]||^{2}1\{||\mathbf{D}_{n,i} -E[\mathbf{D}_{n,i} ]||>\varepsilon \})} \\&\quad =\sum _{i=1}^n {E_{\varvec{\upeta } ^{0}} } \left[ \frac{1}{n}\sum _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j}\log f_i (Y_i |\varvec{\upeta })} \right\} ^{2}}\right. \\&\qquad \left. \left. \times 1\left\{ {\frac{1}{n}\sum _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j } \log f_i (Y_i |\varvec{\upeta })} \right\} ^{2}} > \varepsilon ^{2}} \right\} \right] \right| {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }. \end{aligned}$$

By Assumption (E),

$$\begin{aligned} \frac{1}{n}\sum _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j }\log f_i (Y_i |\varvec{\upeta } ^{0})} \right\} ^{2}} \le \frac{1}{n}\sum _{j=1}^k {A_j^2 (Y_i )} \le \frac{1}{n}\sum _{j=1}^k {\mathop {\sup }\limits _y A_j^2 (y)}. \end{aligned}$$

Hence,

$$\begin{aligned} 1\left\{ {\frac{1}{n}\sum _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j } \log f_i (Y_i |\varvec{\upeta })} \right\} ^{2}} >\varepsilon ^{2}} \right\} \le 1\left\{ {\frac{1}{n}\sum _{j=1}^k {\mathop {\sup }\limits _y A_j^2 (y)} >\varepsilon ^{2}} \right\} , \quad i=1,2,\ldots , n. \end{aligned}$$

It follows that

$$\begin{aligned}&\sum _{i=1}^n {E_{\varvec{\upeta } ^{0}} (||\mathbf{D}_{n,i} -E\mathbf{D}_{n,i} ||^{2}1\{||\mathbf{D}_{n,i} -E\mathbf{D}_{n,i} ||>\varepsilon \})} \\&\quad \le \sum _{i=1}^n {E_{\varvec{\upeta } ^{0}} \left. \left[ {\frac{1}{n}\sum _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j }\log f_i (Y_i |\varvec{\upeta })} \right\} ^{2}1\left\{ {\frac{1}{n}\sum _{j=1}^k {\mathop {\sup }\limits _y A_j^2 (y)} >\varepsilon ^{2}} \right\} ^{2}} } \right] \right| {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} }} \\&\quad =1\left\{ {\frac{1}{n}\sum _{j=1}^k {\mathop {\sup }\limits _y A_j^2 (y)} >\varepsilon ^{2}} \right\} \sum _{i=1}^n {E_{\varvec{\upeta } ^{0}} \left. \left[ {\frac{1}{n}\sum _{j=1}^k {\left\{ {\frac{\partial }{\partial \eta _j }\log f_i (Y_i |\varvec{\upeta })} \right\} ^{2}} } \right] \right| {_{\varvec{\upeta } =\varvec{\upeta } ^{0}} } } \\&\quad =1\left\{ {\frac{1}{n}\sum _{j=1}^k {\mathop {\sup }\limits _y A_j^2 (y)} >\varepsilon ^{2}} \right\} \sum _{j=1}^k {\sum _{i=1}^n {\frac{1}{n}I_{i,jj} (\varvec{\upeta } ^{0})} } \rightarrow 1\{0>\varepsilon ^{2}\}\sum _{j=1}^k {I_{jj} (\varvec{\upeta } ^{0})} =0, \\ \end{aligned}$$

where the last convergence follows from Assumptions (B) and (E). Hence, the Lindeberg condition in Lemma 3 holds. In addition, by Assumption (B),

$$\begin{aligned} \sum _{i=1}^n {\{\mathbf{Cov}_{\varvec{\upeta } ^{0}} (\mathbf{D}_{n,i} )\}_{js} } =\frac{1}{n}\sum _{i=1}^n {I_{i,js} (\varvec{\upeta } ^{0})} \rightarrow I_{js} (\varvec{\upeta } ^{0}). \end{aligned}$$

By Lemma 3 (the Lindeberg–Feller CLT),

$$\begin{aligned} \mathbf{T}_n (\varvec{\upeta } ^{0})=\mathop \sum \nolimits _{i=1}^n {\mathbf{D}_{n,i} } \mathop {\longrightarrow }\limits ^{d}\mathbf{T}(\varvec{\upeta } ^{0})\sim N_k (\mathbf{0},I(\varvec{\upeta } ^{0})). \end{aligned}$$

Step 2 $R_{n,js} (\varvec{\upeta } ^{0})\mathop {\longrightarrow }\limits ^{p}I_{js} (\varvec{\upeta } ^{0})$

Recall that

$$\begin{aligned} R_{n,js} (\varvec{\upeta } ^{0})\equiv & {} -\frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}\\&-\frac{1}{2n}\sum _{l=1}^k {\left\{ {\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } ={\tilde{\varvec{\upeta }}}_n } }} \right\} (\hat{{\eta }}_{ln} -\eta _l^0)}. \end{aligned}$$

By the arguments following Eq. (8),

$$\begin{aligned} -\frac{1}{n}\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } =\varvec{\upeta } ^{0}}}\mathop {\longrightarrow }\limits ^{p}I_{js} (\varvec{\upeta } ^{0}). \end{aligned}$$

Since ${\hat{\varvec{\upeta }}}_n \mathop {\longrightarrow }\limits ^{P}\varvec{\upeta } ^{0}$ and

$$\begin{aligned} \left| {\frac{1}{n}\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\ell _n (\varvec{\upeta }) \left| {_{\varvec{\upeta } ={\tilde{\varvec{\upeta }}}_n } } \right. } \right|= & {} \left| {\frac{1}{n}\sum _{i=1}^n {\gamma _{jsl} (Y_i |{\tilde{\varvec{\upeta }}}_n)} \cdot M_{jsl} (Y_i )} \right| \\\le & {} \frac{1}{n}\sum _{i=1}^n {M_{jsl} (Y_i)} \mathop {\longrightarrow }\limits ^{p}m_{jsl} , \end{aligned}$$

by Slutsky’s theorem,

$$\begin{aligned} -\frac{1}{2n}\sum _{l=1}^k {\left\{ {\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s \partial \eta _l }\ell _n (\varvec{\upeta })\Bigg | {_{\varvec{\upeta } ={\tilde{\varvec{\upeta }}}_n } }} \right\} (\hat{{\eta }}_{ln} -\eta _l^0)} \mathop {\longrightarrow }\limits ^{p}0. \end{aligned}$$

Hence, we have $R_{n,js} (\varvec{\upeta } ^{0})\mathop {\longrightarrow }\limits ^{p}I_{js} (\varvec{\upeta } ^{0})$.

Lemma 5

(Lehmann and Casella 1998) Let $\mathbf{T}_n =(T_{1n}, T_{2n} ,\ldots ,T_{kn} )\mathop {\longrightarrow }\limits ^{d}{} \mathbf{T}=(T_1, T_2 ,\ldots ,T_k )$. Suppose that for fixed j and s, let $R_{jsn}$ be a sequence of random variables, where $R_{jsn} \mathop {\longrightarrow }\limits ^{p}r_{js}$ (constants) for which the matrix $\mathbf{R}$, with each element $r_{js}$, is nonsingular. Let $\mathbf{B}=\mathbf{R}^{-1}$ with each element $b_{js}$. Let $\mathbf{C}_n =(C_{1n}, C_{2n} ,\ldots ,C_{kn})$ be a solution to

$$\begin{aligned} \sum _{s=1}^k {R_{jsn} C_{sn} =T_{jn} } ,\quad j=1,2,\ldots , k, \end{aligned}$$

and let $\mathbf{C}=(C_1, C_2 ,\ldots , C_k)$ be a solution to

$$\begin{aligned} \sum _{s=1}^k {r_{js} C_s =T_j ,} \quad j=1,2,\ldots , k, \end{aligned}$$

given by $C_j = \sum _{s=1}^k {b_{js} T_s }, j = 1,2,\ldots , k$. Then, if the distribution of $(T_1, T_2, \ldots , T_k)$ has a density,

$$\begin{aligned} \mathbf{C}_n =(C_{1n}, C_{2n} ,\ldots , C_{kn} )\mathop {\longrightarrow }\limits ^{d}{} \mathbf{C}=(C_1, C_2 ,\ldots , C_k ), \quad n\rightarrow \infty . \end{aligned}$$

Combining Steps 1–2 with Lemma 5, $\mathbf{C}_n =\sqrt{n}({\hat{\varvec{\upeta }}}_n -\varvec{\upeta } ^{0})$ converges in distribution to $\mathbf{C}$, a solution to

$$\begin{aligned} \sum _{s=1}^k {I_{js} (\varvec{\upeta } ^{0})C_s } =T_j (\varvec{\upeta } ^{0}), \quad j=1,2,\ldots , k, \end{aligned}$$

where $\mathbf{T}(\varvec{\upeta } ^{0})=(T_1 (\varvec{\upeta } ^{0}),T_2 (\varvec{\upeta } ^{0}),\ldots , T_k (\varvec{\upeta } ^{0}))\sim N_k (\mathbf{0},I(\varvec{\upeta } ^{0}))$. Therefore, we have the desired result $\mathbf{C}=[I(\varvec{\upeta } ^{0})]^{-1}\cdot \mathbf{T}(\varvec{\upeta } ^{0})\sim N_k (\mathbf{0},[I(\varvec{\upeta } ^{0})]^{-1})$. $\square$

1.4 Proofs of Lemma 4

Using the notations of “Proof of Lemma 1” in Appendix 1,

$$\begin{aligned} \frac{\partial }{\partial \eta _j }\log f_i (y| \varvec{\upeta })= y^j -\frac{E_i^j (\varvec{\upeta })}{E_i^0 (\varvec{\upeta })},\quad j=1,2,\ldots , k. \end{aligned}$$

Under Assumption (G), $[u_0, v_0 ]\subset [u_i, v_i ]=R_i \subset {{\textsf {y}}}$. Thus,

$$\begin{aligned} E_i^0 (\varvec{\upeta })=\mathop \int \limits _{R_i \cap y} {\exp \{\varvec{\upeta } ^{\mathrm{T}}\cdot \mathbf{t}(y)\}dy} \ge \mathop \int \limits _{u_0 }^{v_0 } {\exp \{\varvec{\upeta } ^{\mathrm{T}}\cdot \mathbf{t}(y)\}dy}. \end{aligned}$$

It follows from Assumption (F) that

$$\begin{aligned} \mathop {\inf }\limits _{\varvec{\upeta } \in \Theta } E_i^0 (\varvec{\upeta })\ge \mathop {\inf }\limits _{\varvec{\upeta } \in \Theta } \mathop \int \limits _{u_0 }^{v_0 } {\exp \{\varvec{\upeta } ^{\mathrm{T}}\cdot \mathbf{t}(y)\}dy} \equiv E_{\mathrm {Inf}}^0 >0, \quad i=1,2,\ldots , n, \end{aligned}$$

Similarly, since all the moments exist,

$$\begin{aligned} \mathop {\sup }\limits _{\varvec{\eta } \in \Theta } |E_i^j (\varvec{\upeta })|\le \mathop {\sup }\limits _{\varvec{\upeta } \in \Theta } \mathop \int \limits _{{\textsf {y}}} {|y|^{j}\exp \{\varvec{\upeta } ^{\mathrm{T}} \cdot \mathbf{t}(y)\}dy} \equiv E_{\mathrm {Sup}}^j <\infty , \quad j=0,1,\ldots , 3k, \end{aligned}$$

for $i=1,2,\ldots , n$. Then, as in “Proof of Lemma 1” in Appendix 1,

$$\begin{aligned} \left| {\frac{\partial ^{2}}{\partial \eta _j \partial \eta _s}\log f_i (y|\varvec{\upeta } )} \right|\le & {} \left| {\frac{E_i^{j+s} (\varvec{\eta })}{E_i^0 (\varvec{\eta } )}-\frac{E_i^j (\varvec{\eta })}{E_i^0 (\varvec{\eta })}\frac{E_i^s (\varvec{\eta })}{E_i^0 (\varvec{\eta })}} \right| \\\le & {} \frac{\sup _\eta |E_i^{j+s} (\varvec{\eta })|}{\inf _\eta E_i^0 (\varvec{\eta })}+\frac{\sup _\eta |E_ i^j (\varvec{\upeta })|}{\inf _\eta E_i^0 (\varvec{\upeta })} \frac{\sup _\eta |E_i^s (\varvec{\upeta })|}{\inf _\eta E_i^0 (\varvec{\upeta })}\\\le & {} \frac{E_{\mathrm {Sup}}^{j+s} }{E_{\mathrm {Inf}}^0 }+\frac{E_{\mathrm {Sup}}^j }{E_{\mathrm {Inf}}^0 }\frac{E_{\mathrm {Sup}}^s }{E_{\mathrm {Inf}}^0 }\equiv W_{js} (y)<\infty . \end{aligned}$$

In this way, one can find all the constant functions $W_{js} (\cdot )$ that satisfy the requirements of Assumption (D). In a similar fashion, Assumption (C) can be checked with

$$\begin{aligned} \left| {\frac{\partial ^{3}}{\partial \eta _j \partial \eta _s^ \partial \eta _l}\log f_i (y|\varvec{\upeta } )} \right|\le & {} \frac{E_{\mathrm {Sup}}^{j+s+l} }{E_{\mathrm {Inf}}^0 }+ \frac{E_{\mathrm {Sup}}^{j+s} }{E_{\mathrm {Inf}}^0 }\frac{E_{\mathrm {Sup}}^l }{E_{\mathrm {Inf}}^0 }+\frac{E_{\mathrm {Sup}}^j }{E_{\mathrm {Inf}}^0 } \frac{E_{\mathrm {Sup}}^{l+s} }{E_{\mathrm {Inf}}^0 } +\frac{E_{\mathrm {Sup}}^l }{E_{\mathrm {Inf}}^0 } \frac{E_{\mathrm {Sup}}^{j+s} }{E_{\mathrm {Inf}}^0 }\\&+2\frac{E_{\mathrm {Sup}}^j }{E_{\mathrm {Inf}}^0 }\frac{E_{\mathrm {Sup}}^s }{E_{\mathrm {Inf}}^0 }\frac{E_{\mathrm {Sup}}^l }{E_{\mathrm {Inf}}^0 }\equiv M_{jsl} (y)<\infty . \end{aligned}$$

To check Assumption (E), we use $|y^j |\le \max \{|u_i^j |,|v_i^j |\}\le \max \{|u_0^*|^{j},|v_0^*|^{j}\}<\infty$ for $u_i \le y\le v_i$. Then,

$$\begin{aligned} \left| {\frac{\partial }{\partial \eta _j} \log f_i (y|\varvec{\upeta } )} \right|\le & {} |y^j |1\{u_i \le y\le v_i \}+\frac{\sup _{\varvec{\eta }} E_i^j (\varvec{\upeta })}{\inf _{\varvec{\eta }} E_i^0 (\varvec{\eta })}\\\le & {} \max \{|u_0^*|^{j},|v_0^*|^{j}\}+ \frac{E_{\mathrm {Sup}}^j }{E_{\mathrm {Inf}}^0 }\equiv A_j (y). \end{aligned}$$

Hence, Assumption (E) holds for the constant function $A_j (\cdot )$.

Appendix 2: Data generations

For the cubic SEF with $\eta _3 >0$, we consider $U^{*}\sim N(\mu _u, 1)$, $V^{*}\sim \min \{N(\mu _v, 1),\tau _2 \}$ and

$$\begin{aligned} Y^{*}\sim f_{\varvec{\eta }} (y)=\exp [\eta _1 y+\eta _2 y^{2}+\eta _3 y^{3}-\phi (\varvec{\eta } )],\quad y\in {{\textsf {y}}}=(-\infty , \tau _2], \end{aligned}$$

where $\phi (\varvec{\eta })=\log \{\int _{{{\textsf {y}}}} {\exp (\eta _1 y+\eta _2 y^{2}+\eta _3 y^{3})dy}\}$. The value $Y^{*}$ is generated by solving

$$\begin{aligned} W^{*}=F_{\varvec{\eta }} (Y^{*})=\frac{\mathop \int \limits _{-\infty }^{Y^{*}} {\exp [\eta _1 y+\eta _2 y^{2}+\eta _3 y^{3}]dy} }{\mathop \int \limits _{-\infty }^{\tau _2 } {\exp [\eta _1 y+\eta _2 y^{2}+\eta _3 y^{3}]dy}}, \end{aligned}$$

where $W^{*}\sim U(0,1)$. Under these models, we know $u_{\inf } =\inf _i (u_i^*)=\inf _i (u_i )=-\infty$ and $v_{\sup } =\sup _i (v_i^*)=\sup _i (v_i )=\tau _2$. Under this setting, Assumption (G) does not hold as $u_{\inf } =-\infty$ is not a finite number. In addition, there is a chance that the length $v_i -u_i$ is quite small. The case of $\eta _3 <0$ is similar. It would be of our interest to study the numerical properties of the MLE under this delicate setting.

We set the sample inclusion probability to be $P(U^{*}\le Y^{*}\le V^{*})\approx 0.5$ or 0.25 by letting $\mu _u =\eta _1 -\Delta$ and $\mu _v =\eta _1 +\Delta$. First, under $\eta _1 =5$, $\eta _2 =-0.5$, $\eta _3 =0.005$ and $\tau _2 =8$, the value is $\Delta =1.01$ (Hu and Emura 2015) to meet $P(U^{*}\le Y^{*}\le V^{*})\approx 0.50$. If we set $\Delta =0.33$ then $P(U^{*}\le Y^{*}\le V^{*})\approx 0.25$. Second, under $\eta _1 =5$, $\eta _2 =-0.5$, $\eta _3 =-0.005$, and $\tau _1 =2$, we set $\Delta =0.91$ (Hu and Emura 2015) to meet $P(U^{*}\le Y^{*}\le V^{*})\approx 0.50$. If we set $\Delta = 0.26$, then $P(U^{*}\le Y^{*}\le V^{*})\approx 0.25$.