Curved shock theory

Abstract

Curved shock theory (CST) is introduced, developed and applied to relate pressure gradients, streamline curvatures, vorticity and shock curvatures in flows with planar or axial symmetry. Explicit expressions are given, in an influence coefficient format, that relate post-shock pressure gradient, streamline curvature and vorticity to pre-shock gradients and shock curvature in steady flow. The effect of pre-shock flow divergence/convergence, on vorticity generation, is related to the transverse shock curvature. A novel derivation for the post-shock vorticity is presented that includes the effects of pre-shock flow non-uniformities. CST applicability to unsteady flows is discussed.

Appendices

Appendix 1. Derivation of the curved shock equation (32)

For nomenclature and methodology refer to Sect. 2.

The pressure ratio across an oblique shock is given by,

$$\begin{aligned}&\frac{p_2 }{p_1 } = \frac{2\gamma }{\gamma +1}M_1^2 \text {sin}^{2}\theta -\frac{\gamma -1}{\gamma +1}\\&\frac{p_2 }{p_1 } = \frac{2\gamma }{\gamma +1}\frac{\rho _1 V_1^2 }{\gamma p_1 }\text {sin}^{2}\theta -\frac{\gamma -1}{\gamma +1}\\&\left( {\gamma +1} \right) p_2 = 2\rho _1 V_1^2 \text {sin}^{2}\theta -\left( {\gamma -1} \right) p_1 \end{aligned}$$

Taking derivatives of both sides with respect to distance along the shock, $\sigma$,

$$\begin{aligned} \left( {\gamma +1} \right) \frac{\partial p_2 }{\partial \sigma }= & {} 2\rho _1 V_1^2 \frac{\partial \text {sin}^{2}\theta }{\partial \sigma }+2\rho _1 \text {sin}^{2}\theta \frac{\partial V_1^2 }{\partial \sigma }\\&+2V_1^2 \text {sin}^{2}\theta \frac{\partial \rho _1 }{\partial \sigma }-\left( {\gamma -1} \right) \frac{\partial p_1 }{\partial \sigma } \end{aligned}$$

Changing $\sigma$ derivatives to s and n derivatives,

$$\begin{aligned}&\left( {\gamma +1} \right) \left[ {\frac{\partial p_2 }{\partial s}\text {cos}\left( {\theta -\delta } \right) +\frac{\partial p_2 }{\partial n}\text {sin}\left( {\theta -\delta } \right) } \right] \nonumber \\&\quad =4\text {sin}\theta \text {cos}\theta \rho _1 V_1^2 \frac{\partial \theta }{\partial \sigma }\nonumber \\&\qquad +\,4V_1 \rho _1 \text {sin}^{2}\theta \left( {\frac{\partial V_1 }{\partial s}\text {cos}\theta +\frac{\partial V_1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\qquad +\,2V_1^2 \text {sin}^{2}\theta \left( {\frac{\partial \rho _1 }{\partial s}\text {cos}\theta +\frac{\partial \rho _1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\qquad -\,\left( {\gamma -1} \right) \left( {\frac{\partial p_1 }{\partial s}\text {cos}\theta +\frac{\partial p_1 }{\partial n}\text {sin}\theta } \right) \end{aligned}$$

(49)

Derivatives $\frac{\partial \theta }{\partial \sigma },\frac{\partial {\bullet }}{\partial \hbox {s}}$ and $\frac{\partial {\bullet }}{\partial \hbox {n}}$ can be expressed as:

$$\begin{aligned}&\frac{\partial p_1 }{\partial \hbox {s}}=P_1 \rho _1 V_1^2 \quad \quad \frac{\partial p_2 }{\partial \hbox {s}}=P_2 \rho _2 V_2^2\\&\frac{\partial p_1 }{\partial \hbox {n}}=-D_1 \rho _1 V_1^2 \quad \quad \frac{\partial p_2 }{\partial \hbox {n}}=-D_2 \rho _2 V_2^2\\&\frac{\partial V_1 }{\partial \hbox {s}}=-P_1 V_1 \quad \quad \frac{\partial V_1 }{\partial \hbox {n}}=V_1 \left( {D_1 -\Gamma _1 } \right) \\&\frac{\partial \rho _1 }{\partial \hbox {s}}=\rho _1 M_1^2 P_1 \quad \quad \frac{\partial \rho _1 }{\partial \hbox {n}}=-\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \\&\frac{\partial \theta }{\partial \sigma }=S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1 -\text {cos}\theta D_1 +\frac{\text {sin}\theta \text {sin}\delta _1 }{y} \end{aligned}$$

With these substitutions (49) becomes,

$$\begin{aligned}&\left( {\gamma +1} \right) \left[ {P_2 \rho _2 V_2^2 \text {cos}\left( {\theta -\delta } \right) -D_2 \rho _2 V_2^2 \text {sin}\left( {\theta -\delta } \right) } \right] \nonumber \\&\quad =4\text {sin}\theta \text {cos}\theta \rho _1 V_1^2 \left[ S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1\right. \nonumber \\&\left. \qquad -\,\text {cos}\theta D_1 +\frac{\text {sin}\theta \text {sin}\delta _1 }{y} \right] \nonumber \\&\qquad +\,4V_1 \rho _1 \text {sin}^{2}\theta \left[ {-P_1 V_1 \text {cos}\theta +V_1 \left( {D_1 -\Gamma _1 } \right) \text {sin}\theta } \right] \nonumber \\&\qquad +\,2V_1^2 \text {sin}^{2}\theta \left\{ \rho _1 M_1^2 P_1 \text {cos}\theta \right. \nonumber \\&\qquad \left. -\,\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \text {sin}\theta \right\} \nonumber \\&\qquad -\,\left( {\gamma -1} \right) \left( {P_1 \rho _1 V_1^2 \text {cos}\theta -D_1 \rho _1 V_1^2 \text {sin}\theta } \right) \end{aligned}$$

(50)

Replacing $\frac{1}{y} \hbox { by}-\frac{S_b }{\text {cos}\theta _1 } \left( {\frac{1}{y}=-\frac{S_b }{\text {cos}\theta _1 }} \right)$, (50) becomes,

$$\begin{aligned}&\left( {\gamma +1} \right) \left[ {P_2 \rho _2 V_2^2 \text {cos}\left( {\theta -\delta } \right) -D_2 \rho _2 V_2^2 \text {sin}\left( {\theta -\delta } \right) } \right] \\&\quad =4\text {sin}\theta \text {cos}\theta \rho _1 V_1^2 \left[ S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1\right. \\&\left. \qquad -\,\text {cos}\theta D_1 -\frac{S_b \text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 } \right] \\&\qquad +\,4V_1 \rho _1 \text {sin}^{2}\theta \left[ {-P_1 V_1 \text {cos}\theta +V_1 \left( {D_1 -\Gamma _1 } \right) \text {sin}\theta } \right] \\&\qquad +\,2V_1^2 \text {sin}^{2}\theta \left\{ \rho _1 M_1^2 P_1 \text {cos}\theta \right. \\&\left. \qquad -\,\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \text {sin}\theta \right\} \\&\qquad -\,\left( {\gamma -1} \right) \left( {P_1 \rho _1 V_1^2 \text {cos}\theta -D_1 \rho _1 V_1^2 \text {sin}\theta } \right) \end{aligned}$$

Collecting terms,

$$\begin{aligned}&\left[ -4\rho _1 V_1^2 \left( {M_1^2 -1} \right) \text {sin}^{2}\theta \text {cos}\theta +4\rho _1 V_1^2 \text {sin}^{2}\theta \text {cos}\theta \right. \\&\left. \quad \quad -\,2\rho _1 V_1^2 M_1^2 \text {sin}^{2}\theta \text {cos}\theta +\left( {\gamma -1} \right) \rho _1 V_1^2 \text {cos}\theta \right] P_1 \\&\quad \quad +\,\left[ 4\rho _1 V_1^2 \text {sin}\theta \text {cos}^{2}\theta -4\rho _1 V_1^2 \text {sin}^{3}\theta \right. \\&\quad \quad \left. +\,2\rho _1 V_1^2 M_1^2 \text {sin}^{3}\theta -\left( {\gamma -1} \right) \rho _1 V_1^2 \text {sin}\theta \right] D_1 \\&\quad \quad +\,\left[ {4\rho _1 V_1^2 \text {sin}^{3}\theta +2\left( {\gamma -1} \right) \rho _1 V_1^2 M_1^2 \text {sin}^{3}\theta } \right] \Gamma _1 \\&\quad =\left[ {-\left( {\gamma +1} \right) \rho _2 V_2^2 \text {cos}\left( {\theta -\delta } \right) } \right] P_2\\&\quad \quad +\,\left[ {\left( {\gamma +1} \right) \rho _2 V_2^2 \text {sin}\left( {\theta -\delta } \right) } \right] D_2 \\&\quad \quad +\,\left( {4\rho _1 V_1^2 \text {sin}\theta \text {cos}\theta } \right) S_a \\&\quad \quad +\left[ {-\frac{4\rho _1 V_1^2 \text {sin}^{2}\theta \text {cos}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }} \right] S_b \end{aligned}$$

Dividing through by $\rho _1 V_1^2$,

$$\begin{aligned}&\left[ -4\left( {M_1^2 -1} \right) \text {sin}^{2}\theta \text {cos}\theta +4\text {sin}^{2}\theta \text {cos}\theta \right. \\&\left. \quad -\,2M_1^2 \text {sin}^{2}\theta \text {cos}\theta +\left( {\gamma -1} \right) \text {cos}\theta \right] P_1 \\&\quad +\,\left[ {4\text {sin}\theta \text {cos}^{2}\theta -4\text {sin}^{3}\theta +2M_1^2 \text {sin}^{3}\theta -\left( {\gamma -1} \right) \text {sin}\theta } \right] D_1 \\&\quad +\,\left[ {4\text {sin}^{3}\theta +2\left( {\gamma -1} \right) M_1^2 \text {sin}^{3}\theta } \right] \Gamma _1 \\&\,=\left[ {-\left( {\gamma +1} \right) \frac{\text {sin}\theta \text {cos}\theta }{\text {sin}\left( {\theta -\delta } \right) }} \right] P_2\\&\quad +\,\left[ {\left( {\gamma +1} \right) \frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }} \right] D_2 +\left( {4\text {sin}\theta \text {cos}\theta } \right) S_a \\&\quad +\,\left[ {-\frac{4\text {sin}^{2}\theta \text {cos}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }} \right] S_b \end{aligned}$$

Thus, the curved shock equation (32),

$$\begin{aligned} A_1 P_1 +B_1 D_1 +E_1 \Gamma _1 =A_2 P_2 +B_2 D_2 +CS_a +GS_b \end{aligned}$$

has the coefficients $A_{1}, B_{1}, E_{1}, A_{2}, B_{2}, C$, and G, given by,

$$\begin{aligned} A_1= & {} \frac{4\left( {M_1^2 -1} \right) \text {sin}^{2}\theta \text {cos}\theta -4\text {sin}^{2}\theta \text {cos}\theta +2M_1^2 \text {sin}^{2}\theta \text {cos}\theta -\left( {\gamma -1} \right) \text {cos}\theta }{\gamma +1}\\= & {} \frac{2\text {cos}\theta \left[ {\left( {3M_1^2 -4} \right) \text {sin}^{2}\theta -\left( {\gamma -1} \right) /2} \right] }{\gamma +1}\\ B_1= & {} \frac{-4\text {sin}\theta \text {cos}^{2}\theta +4\text {sin}^{3}\theta -2M_1^2 \text {sin}^{3}\theta +\left( {\gamma -1} \right) \text {sin}\theta }{\gamma +1}\\= & {} \frac{4\text {sin}\theta \left( {\text {sin}^{2}\theta -1} \right) +4\text {sin}^{3}\theta -2M_1^2 \text {sin}^{3}\theta +\left( {\gamma -1} \right) \text {sin}\theta }{\gamma +1}\\= & {} \frac{2\text {sin}\theta \left[ {\left( {\gamma -5} \right) /2+\left( {4-M_1^2 } \right) \text {sin}^{2}\theta } \right] }{\gamma +1}\\ E_1= & {} \frac{-4\text {sin}^{3}\theta -2\left( {\gamma -1} \right) M_1^2 \text {sin}^{3}\theta }{\gamma +1}\\= & {} -\frac{2\text {sin}^{3}\theta \left[ {2+\left( {\gamma -1} \right) M_1^2 } \right] }{\gamma +1}\\ A_2= & {} \frac{\text {sin}\theta \text {cos}\theta }{\text {sin} \left( {\theta -\delta } \right) }\\ B_2= & {} -\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }\\ \hbox {C}= & {} -\frac{4\text {sin}\theta \text {cos}\theta }{\gamma +1}\\ \hbox {G}= & {} \frac{4\text {sin}^{2}\theta \text {cos}\theta \text {sin}\delta _1 }{\left( {\gamma +1} \right) \text {cos}\theta _1 } \end{aligned}$$

These coefficients can be further simplified by dividing all of them through by $\text {sin}\theta$.

Appendix 2. Derivation of the curved shock equation (33)

Starting from (26), (27) and (28),

$$\begin{aligned}&p_1 +\rho _1 V_1^2 \text {sin}^{2}\theta = p_2 +\rho _2 V_2^2 \text {sin}^{2}\left( {\theta -\delta } \right) \\&p_1 -p_2 = \rho _1 V_1^2 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -\rho _1 V_1^2 \text {sin}^{2}\theta \end{aligned}$$

Taking derivatives of both sides with respect to $\sigma$,

$$\begin{aligned} \frac{\partial p_1 }{\partial \sigma }-\frac{\partial p_2 }{\partial \sigma }= & {} \rho _1 V_1^2 \text {sin}\theta \text {cos}\theta \frac{\partial \tan \left( {\theta -\delta } \right) }{\partial \sigma }\\&+\,\rho _1 V_1^2 \text {sin}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \text {cos}\theta }{\partial \sigma } \\&+\,\rho _1 V_1^2 \text {cos}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \text {sin}\theta }{\partial \sigma }\\&+\,\rho _1 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \frac{\partial V_1^2 }{\partial \sigma } \\&+\,V_1^2 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \rho _1 }{\partial \sigma }\\&-\rho _1 V_1^2 \frac{\partial \text {sin}^{2}\theta }{\partial \sigma }\\&-\,\rho _1 \text {sin}^{2}\theta \frac{\partial V_1^2 }{\partial \sigma }-V_1^2 \text {sin}^{2}\theta \frac{\partial \rho _1 }{\partial \sigma } \\ \end{aligned}$$

Changing to s and n derivatives,

$$\begin{aligned}&\left( {\frac{\partial p_1 }{\partial s}\text {cos}\theta +\frac{\partial p_1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\quad \quad -\,\left[ {\frac{\partial p_2 }{\partial s}\text {cos}\left( {\theta -\delta } \right) +\frac{\partial p_2 }{\partial n}\text {sin}\left( {\theta -\delta } \right) } \right] \nonumber \\&\quad \,=\rho _1 V_1^2 \text {sin}\theta \text {cos}\theta \frac{1}{\text {cos}^{2}\left( {\theta -\delta } \right) }\frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma }\nonumber \\&\quad \quad -\,\rho _1 V_1^2 \text {sin}^{2}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \theta }{\partial \sigma } \nonumber \\&\quad \quad +\,\rho _1 V_1^2 \text {cos}^{2}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \theta }{\partial \sigma }\nonumber \\&\quad \quad +\,2\rho _1 V_1 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \left( {\frac{\partial V_1 }{\partial s}\text {cos}\theta +\frac{\partial V_1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\quad \quad +\,V_1^2 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \left( {\frac{\partial \rho _1 }{\partial s}\text {cos}\theta +\frac{\partial \rho _1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\quad \quad -2\text {sin}\theta \text {cos}\theta \rho _1 V_1^2 \frac{\partial \theta }{\partial \sigma } \nonumber \\&\quad \quad -2\rho _1 V_1 \text {sin}^{2}\theta \left( {\frac{\partial V_1 }{\partial s}\text {cos}\theta +\frac{\partial V_1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\quad \quad -V_1^2 \text {sin}^{2}\theta \left( {\frac{\partial \rho _1 }{\partial s}\text {cos}\theta +\frac{\partial \rho _1 }{\partial n}\text {sin}\theta } \right) \end{aligned}$$

(51)

Derivatives $\frac{\partial \theta }{\partial \sigma },\frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma },\frac{\partial {\bullet }}{\partial {s}}$ and $\frac{\partial {\bullet }}{\partial {n}}$ can be expressed as,

$$\begin{aligned}&\frac{\partial p_1 }{\partial {s}}=P_1 \rho _1 V_1^2 \quad \quad \frac{\partial p_2 }{\partial {s}}=P_2 \rho _2 V_2^2\\&\frac{\partial p_1 }{\partial {n}}=-D_1 \rho _1 V_1^2 \quad \quad \frac{\partial p_2 }{\partial {n}}=-D_2 \rho _2 V_2^2\\&\frac{\partial V_1 }{\partial {s}}=-P_1 V_1 \quad \quad \frac{\partial V_1 }{\partial {n}}=V_1 \left( {D_1 -\Gamma _1 } \right) \\&\frac{\partial \rho _1 }{\partial {s}}=\rho _1 M_1^2 P_1 \quad \quad \frac{\partial \rho _1 }{\partial {n}}=-\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \\&\frac{\partial \theta }{\partial \sigma }=S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1 -\text {cos}\theta D_1 +\frac{\text {sin}\theta \text {sin}\delta _1 }{y}\\&\frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma }=S_a +\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) P_2 -\text {cos} \left( {\theta -\delta } \right) D_2\\&\qquad +\,\frac{\text {sin} \left( {\theta -\delta } \right) \text {sin}\delta _2 }{y} \end{aligned}$$

So (51) becomes,

$$\begin{aligned}&\left( {\rho _1 V_1^2 P_1 \text {cos}\theta -\rho _1 V_1^2 D_1 \text {sin}\theta } \right) \nonumber \\&\quad \quad -\,\left[ {\rho _2 V_2^2 P_2 \text {cos}\left( {\theta -\delta } \right) -\rho _2 V_2^2 D_2 \text {sin}\left( {\theta -\delta } \right) } \right] \nonumber \\&\quad =\frac{\rho _1 V_1^2 \text {sin}\theta \text {cos}\theta }{\text {cos}^{2}\left( {\theta -\delta } \right) }\left[ S_a +\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) P_2\right. \nonumber \\&\left. \quad \quad -\text {cos} \left( {\theta -\delta } \right) D_2 +\frac{\text {sin} \left( {\theta -\delta } \right) \text {sin}\delta _2 }{y} \right] \nonumber \\&\quad \quad +\,\left[ \rho _1 V_1^2 \text {cos}^{2}\theta \tan \left( {\theta -\delta } \right) -\rho _1 V_1^2 \text {sin}^{2}\theta \tan \left( {\theta -\delta } \right) \right. \nonumber \\&\left. \qquad -2\rho _1 V_1^2 \text {sin}\theta \text {cos}\theta \right] \left[ S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1\right. \nonumber \\&\left. \qquad -\text {cos}\theta D_1 +\frac{\text {sin}\theta \text {sin}\delta _1 }{y} \right] \nonumber \\&\quad \quad +\,\left[ {2\rho _1 V_1 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -2\rho _1 V_1 \text {sin}^{2}\theta } \right] \nonumber \\&\quad \quad \times \,\left[ {-P_1 V_1 \text {cos}\theta +V_1 \left( {D_1 -\Gamma _1 } \right) \text {sin}\theta } \right] \nonumber \\&\quad \quad +\,\left[ {V_1^2 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -V_1^2 \text {sin}^{2}\theta } \right] \nonumber \\&\quad \quad \times \,\left\{ {\rho _1 M_1^2 P_1 \text {cos}\theta -\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \text {sin}\theta } \right\} \nonumber \\ \end{aligned}$$

(52)

Replacing $\frac{1}{y}\hbox { by }-\frac{S_b }{\text {cos}\theta _1 }$, (52) becomes,

$$\begin{aligned}&\left[ {\frac{\text {sin}\theta \text {cos}\theta }{\text {sin}\left( {\theta -\delta } \right) }P_2 -\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }D_2 } \right] \\&\quad \,=\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}^{2}\left( {\theta -\delta } \right) }\left[ S_a +\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) P_2\right. \\&\quad \left. \quad -\text {cos} \left( {\theta -\delta } \right) D_2 -\frac{S_b \text {sin} \left( {\theta -\delta } \right) \text {sin}\delta _2 }{\text {cos}\theta _1 } \right] \\&\quad \quad +\,\left[ {\text {cos}^{2}\theta \tan \left( {\theta -\delta } \right) -\text {sin}^{2}\theta \tan \left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta } \right] \\&\quad \quad \times \,\left[ {S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1 -\text {cos}\theta D_1 -\frac{S_b \text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }} \right] \\&\quad \quad +\,\left[ {2\text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -2\text {sin}^{2}\theta } \right] \\&\qquad \times \,\left[ {-P_1 \text {cos}\theta +\left( {D_1 -\Gamma _1 } \right) \text {sin}\theta } \right] \\&\quad \quad +\,\left[ {\text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -\text {sin}^{2}\theta } \right] \left\{ M_1^2 P_1 \text {cos}\theta \right. \\&\left. \qquad -M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \text {sin}\theta \right\} \end{aligned}$$

Collecting terms,

$$\begin{aligned}&\left\{ \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) -\left( {M_1^2 -1} \right) \text {sin}\theta \left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \right. \\&\left. \left. \quad \quad -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \right. \\&\left. \quad \quad +\,\text {cos}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right. \\&\left. \quad \quad -\,\!M_1^2 \text {cos}\theta \left[ {\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right\} P_1 \\&\quad \qquad +\,\left\{ -\text {sin}\theta \text {cos}\left( {\theta -\delta } \right) +\text {cos}\theta \left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \right. \\&\left. \left. \qquad -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \right. \\&\left. \quad \quad -\text {sin}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right. \\&\left. \quad \quad +\,\!M_1^2 \text {sin}\theta \left[ {\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right\} D_1 \\&\quad \quad +\,\left\{ \text {sin}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right. \\&\quad \,\,\,\, \left. +\,\left( {\gamma -1} \right) M_1^2 \text {sin}\theta \left[ \text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) \right. \right. \\&\left. \left. \quad \,\,\,\, -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) \right] \right\} \Gamma _1 \end{aligned}$$

$$\begin{aligned}&\,=\left[ \frac{\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) }{\text {sin}\left( {\theta -\delta } \right) }\right. \\&\left. \quad +\,\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) \right] P_2\\&\quad +\,\left[ {-2\text {sin}\theta \text {cos}\theta } \right] D_2 \\&\quad +\,\left[ \frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }+\text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. \quad -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] S_a \\&\quad +\,\left\{ -\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }\frac{\text {sin} \left( {\theta -\delta } \right) \text {sin}\delta _2 }{\text {cos}\theta _1 }\right. \\&\left. \quad -\,\frac{\text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }\left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \right. \\&\left. \left. \quad -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \right\} S_b \end{aligned}$$

The curved shock equation (33),

$$\begin{aligned} A_1^{\prime } P_1 +B_1^{\prime } D_1 +E_1^{\prime } \Gamma _1 =A_2^{\prime } P_2 +B_2^{\prime } D_2 +{C}^{\prime }S_{a} +G^{\prime }S_{b} \end{aligned}$$

where the coefficients $A_1^{\prime }, B_1^{\prime }, E_{1}^{\prime }, A_2^{\prime }, B_2^{\prime },{C}^{\prime },G^{\prime }$ are given by,

$$\begin{aligned} A_1^{\prime }= & {} \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) -\left( {M_1^2 -1} \right) \text {sin}\theta \left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \\&+\,\text {cos}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\&-\,M_1^2 \text {cos}\theta \left[ {\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\= & {} \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) +\left( {M_1^2 -1} \right) \text {sin}\theta \text {sin}\left( {\theta +\delta } \right) \\&+\,M_1^2 \text {sin}\theta \text {cos}\theta \text {sin}\delta -2\text {sin}\theta \text {cos}\theta \text {sin}\delta \\= & {} \text {cos}\theta \left( {\text {cos}\theta \text {cos}\delta +\text {sin}\theta \text {sin}\delta } \right) \\&+\,\left( {M_1^2 -1} \right) \text {sin}\theta \left( {\text {sin}\theta \text {cos}\delta +\text {sin}\delta \text {cos}\theta } \right) \\&+\,M_1^2 \text {sin}\theta \text {cos}\theta \text {sin}\delta -2\text {sin}\theta \text {cos}\theta \text {sin}\delta \\= & {} 2M_1^2 \text {sin}\theta \text {cos}\theta \text {sin}\delta -2\text {sin}\theta \text {cos}\theta \text {sin}\delta \\&+\,M_1^2 \text {sin}^{2}\theta \text {cos}\delta +\text {cos}^{2}\theta \text {cos}\delta -\text {cos}\delta \text {sin}^{2}\theta \\= & {} \left( {M_1^2 -1} \right) \text {sin}2\theta \text {sin}\delta +\left( {M_1^2 -1} \right) \text {sin}^{2}\theta \text {cos}\delta \\&+\,\left( {M_1^2 -1} \right) \text {cos}^{2}\theta \text {cos}\delta -\left( {M_1^2 -1} \right) \text {cos}^{2}\theta \text {cos}\delta \\&+\,\text {cos}^{2}\theta \text {cos}\delta \\= & {} M_1^2 \text {cos}^{2}\theta \text {cos}\delta -\left( {M_1^2 -1} \right) \text {cos}\left( {2\theta +\delta } \right) \\ B_1^{\prime }= & {} -\text {sin}\theta \text {cos}\left( {\theta -\delta } \right) +\text {cos}\theta \left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \\&-\text {sin}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\&+\,\!M_1^2 \text {sin}\theta \left[ {\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\= & {} -\text {sin}\theta \text {cos}\left( {\theta -\delta } \right) -\text {cos}\theta \text {sin}\left( {\theta +\delta } \right) \\&+\,2\text {sin}^{2}\theta \text {sin}\delta -M_1^2 \text {sin}^{2}\theta \text {sin}\delta \\= & {} -\text {sin}\left( {2\theta +\delta } \right) -M_1^2 \text {sin}^{2}\theta \text {sin}\delta \end{aligned}$$

$$\begin{aligned} E_1^{\prime }= & {} \text {sin}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\&+\,\left( {\gamma -1} \right) M_1^2 \text {sin}\theta \left[ \text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. -\,\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) \right] \\= & {} -\left[ {2+\left( {\gamma -1} \right) M_1^2 } \right] \text {sin}\delta \text {sin}^{2}\theta \\ A_2^{\prime }= & {} \frac{\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) }{\text {sin}\left( {\theta -\delta } \right) }+\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) \\= & {} \frac{\text {sin}\theta \text {cos}\theta \text {cos}^{2}\left( {\theta -\delta } \right) +\text {sin}\theta \text {cos}\theta \left( {M_2^2 -1} \right) \text {sin}^{2}\left( {\theta -\delta } \right) }{\text {sin}\left( {\theta -\delta } \right) \text {cos}\left( {\theta -\delta } \right) }\\= & {} \frac{\left[ {1+\left( {M_2^2 -2} \right) \text {sin}^{2}\left( {\theta -\delta } \right) } \right] \text {sin}\theta \text {cos}\theta }{\text {sin}\left( {\theta -\delta } \right) \text {cos}\left( {\theta -\delta } \right) } \end{aligned}$$

$$\begin{aligned} B_2^{\prime }= & {} -2\text {sin}\theta \text {cos}\theta =-\text {sin}\left( {2\theta } \right) \\ C^{\prime }= & {} \frac{{\text {sin}\theta \text {cos}\theta }}{{\text {cos}\left( {\theta - \delta } \right) }} + \text {cos}^{2} \theta {\text {sin}}\left( {\theta - \delta } \right) - \text {sin}^{2} \theta {\text {sin}}\left( {\theta - \delta } \right) \\&- 2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta - \delta } \right) \\= & {} \frac{{\text {sin}\theta \text {cos}\theta + \text {cos}2\theta {\text {sin}}\left( {\theta - \delta } \right) \text {cos}\left( {\theta - \delta } \right) - \text {sin}2\theta \text {cos}^{2} \left( {\theta - \delta } \right) }}{{\text {cos}\left( {\theta - \delta } \right) }}\\= & {} \frac{{\text {sin}\theta \text {cos}\theta - \text {sin}\left( {\theta + \delta } \right) \text {cos}\left( {\theta - \delta } \right) }}{{\text {cos}\left( {\theta - \delta } \right) }}\\= & {} \frac{{ - \text {sin}\left( {2\delta } \right) }}{{2\text {cos}\left( {\theta - \delta } \right) }}\\ G^{\prime }= & {} - \frac{{\text {sin}\theta \text {cos}\theta }}{{\text {cos}\left( {\theta - \delta } \right) }}\frac{{\text {sin} \left( {\theta - \delta } \right) \text {sin}\delta _{2} }}{{\text {cos}\theta _{1} }}\\&-\,\frac{\text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }\left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. -\,2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \\= & {} -\frac{\text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \text {sin}\delta _2 }{\text {cos}\theta _1 }+\frac{\text {sin}\left( {\theta +\delta } \right) \text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }\\= & {} -\frac{\text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \text {sin}\delta _2 -\text {sin}\left( {\theta +\delta } \right) \text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 } \end{aligned}$$

Appendix 3. Derivation of the equation for vorticity behind a curved shock

Although the effect of pre-shock vorticity on the post-shock flow curvature and pressure gradient is included in the curved shock equations (32, 33), the post-shock vorticity does not appear explicitly. For example, when applying CST to RR and MR, the post-shock vorticity, in region (2), behind the incident shock, is required as input to the curvature calculations of the reflected shock when a curved incident shock has created vorticity in front of the reflected shock.

The vorticity behind a curved shock, as given by Truesdell [28], and more recently by Emanuel [4] is,

$$\begin{aligned} \omega _2 =V_1 \frac{\rho _2 }{\rho _1 }\left( {1-\frac{\rho _1 }{\rho _2 }} \right) ^{2}\cos \theta \times \frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(53)

The derivation of this equation uses the Crocco relation between vorticity and entropy and assumes a uniform upstream flow. The normalized version of (53) is,

$$\begin{aligned} \Gamma _2 =\frac{\omega _2 }{V_2 }=\frac{V_1 }{V_2 }\frac{\rho _2 }{\rho _1 }\left( {1-\frac{\rho _1 }{\rho _2 }} \right) ^{2}\cos \theta \times \frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(54)

Equation (54) can be further simplified using the oblique shock relations:

$$\begin{aligned} \Gamma _2 =\frac{2\sin ^{2}\delta }{\sin (2\theta )\sin (\theta -\delta )}\frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(55)

This equation gives the normalized vorticity behind an acute or obtuse shock with aerodynamic curvature $\frac{\partial \theta }{\partial \sigma }$ when the upstream flow is uniform and irrotational. The aerodynamic curvature consists of the geometric curvature and the pre-shock flow divergence/convergence according to $\frac{\partial \theta }{\partial \sigma }=\frac{\partial \theta _1 }{\partial \sigma }-\frac{\partial \delta _1 }{\partial \sigma }$.

We seek an expression for vorticity behind a doubly curved shock for a shock that faces a flow that is curved, has a pressure gradient, is vorticial and is converging or diverging towards or away from the line of symmetry—altogether a very high degree of generality. As for the previous derivations, the flow is steady and of a calorically and thermally perfect gas. Results apply directly to flows that possess axial and planar symmetry and with some considerations of symmetry also to curved shock elements in three-dimensional flow. As for $P_{2}$ and $D_{2}$ derivations, we derive the rational as well as the influence coefficient forms of the vorticity equation. The derivation is based on the shock-tangential momentum equation, the Euler equations and the definition of vorticity for the upstream (subscript 1) and downstream (subscript 2) flows. The following Euler relations are used to eliminate derivatives of velocity in favour of expressions containing streamwise pressure gradient, streamline curvature and normalized vorticity,

$$\begin{aligned} \begin{aligned}&\frac{1}{V_1 }\left( {\frac{\partial V}{\partial s}} \right) _1 =-P_1 \qquad \frac{1}{V_1 }\left( {\frac{\partial V}{\partial n}} \right) _1 =D_1 -\Gamma _1 \\&\frac{1}{V_2 }\left( {\frac{\partial V}{\partial s}} \right) _2 =-P_{2} \qquad \frac{1}{V_2 }\left( {\frac{\partial V}{\partial n}} \right) _2 =D_2 -\Gamma _2 \end{aligned} \end{aligned}$$

(56)

The geometric shock angle is $\theta _1 =\theta +\delta _1$. Taking derivatives of $\theta _1$ with respect to $\sigma$ gives the geometric shock curvature in the flow plane, $S_a$,

$$\begin{aligned} S_a =\frac{\partial \theta _1 }{\partial \sigma }=\frac{\partial \theta }{\partial \sigma }+\frac{\partial \delta _1 }{\partial \sigma } \end{aligned}$$

(57)

This can be written,

$$\begin{aligned} S_a =\frac{\partial \theta }{\partial \sigma }+\cos \theta \frac{\partial \delta _1 }{\partial s}+\sin \theta \frac{\partial \delta _1 }{\partial n} \end{aligned}$$

(58)

But

$$\begin{aligned} \frac{\partial \delta _1 }{\partial s}=D_1 \hbox { and }\frac{\partial \delta _1 }{\partial n}=-\left( {M_1^2 -1} \right) P_1 -\sin \delta _1 /y \end{aligned}$$

(59)

So that,

$$\begin{aligned} \frac{\partial \theta }{\partial \sigma }=S_a +\left( {M_1 ^{2}-1} \right) \sin \theta P_1 -\cos \theta D_1 +\sin \theta \sin \delta _1 /y\nonumber \\ \end{aligned}$$

(60)

Similarly, starting from $\theta -\delta =\theta _1 -\delta _2$ gives,

$$\begin{aligned} \frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma }= & {} S_a +\left( {M_2 ^{2}-1} \right) \sin \left( {\theta -\delta } \right) P_2 -\cos \left( {\theta -\delta } \right) D_2\nonumber \\&+\sin \left( {\theta -\delta } \right) \sin \delta _2 /y \end{aligned}$$

(61)

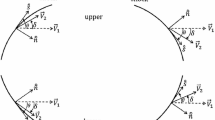
In these equations $\delta _1$ and $\delta _2$ are the geometric flow inclinations in front of and behind the shock. $\delta =\delta _2 -\delta _1$ is the flow deflection through the shock and $\theta$ is the corresponding aerodynamic shock angle. $\theta _1$ is the geometric (physical) shock inclination. All inclinations are measured from the axis of symmetry, in the flow plane. For axial flow, y is the perpendicular distance from the shock to the axis of symmetry or, more generally, the radius of curvature of the shock trace in the transverse plane. For planar flow $y\rightarrow \infty$. Equations (11) and (15) are needed in the derivation of the vorticity equation. The derivation follows.

The momentum equation tangential to the shock is,

$$\begin{aligned} V_1 \cos \theta =V_2 \cos \left( {\theta -\delta } \right) . \end{aligned}$$

(62)

Taking derivatives of both sides of this equation with respect to the distance $\sigma$ along the shock gives,

$$\begin{aligned} V_1 \frac{\partial \cos \theta }{\partial \sigma }\,+\,\cos \theta \frac{\partial V_1 }{\partial \sigma }\,=\,V_2 \frac{\partial \cos \left( {\theta -\delta } \right) }{\partial \sigma }\,+\,\cos \left( {\theta -\delta } \right) \frac{\partial V_2 }{\partial \sigma } \end{aligned}$$

Dividing through by $V_{1}$ and using equations (56) and (59) gives,

$$\begin{aligned}&\sin \theta \frac{\partial \theta }{\partial \sigma }-\cos \theta \left[ {\cos \theta \frac{1}{V_1 }\left( {\frac{\partial V}{\partial s}} \right) _1 +\sin \theta \frac{1}{V_1 }\left( {\frac{\partial V}{\partial n}} \right) _1 } \right] \nonumber \\&\quad =\frac{V_2 }{V_1 }\left[ {\sin \left( {\theta -\delta } \right) \frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma }} \right] \nonumber \\&\qquad -\cos \left( {\theta -\delta } \right) \frac{V_2 }{V_1 }\left[ \cos \left( {\theta -\delta } \right) \frac{1}{V_2 }\left( {\frac{\partial V}{\partial s}} \right) _2\right. \nonumber \\&\left. \qquad +\sin \left( {\theta -\delta } \right) \frac{1}{V_2 }\left( {\frac{\partial V}{\partial n}} \right) _2 \right] \end{aligned}$$

(63)

Using (11) and (15) to replace the velocity and angle derivatives and replacing $V_2 /V_1$ by $\cos \theta {/}\cos \left( {\theta -\delta } \right)$ gives,

$$\begin{aligned}&\sin \theta \left[ {S_a +\left( {M_1^2 -1} \right) \sin \theta P_1 -\cos \theta D_1 +\sin \theta \sin \delta _1 /y} \right] \nonumber \\&\qquad +\cos ^{2}\theta P_1 -\cos \theta \sin \theta \left\{ {D_1 -\Gamma _1 } \right\} \nonumber \\&\quad =\cos \theta \tan \left( {\theta -\delta } \right) \left[ S_a +\left( {M_2^2 -1} \right) \sin \left( {\theta -\delta } \right) P_2\right. \nonumber \\&\left. \qquad -\cos \left( {\theta -\delta } \right) D_2 +\sin \left( {\theta -\delta } \right) \sin \delta _2 /y \right] \nonumber \\&\qquad -\cos \theta \left[ {-\cos \left( {\theta -\delta } \right) P_2 +\sin \left( {\theta -\delta } \right) \left\{ {D_2 -\Gamma _2 } \right\} } \right] \nonumber \\ \end{aligned}$$

(64)

Dividing through by $\cos \theta$ and collecting coefficients of the physical variables $P_{1}, D_{1}$ etc. results in the vorticity equation,

(65)

where,

$$\begin{aligned} \begin{aligned}&{A}_1^{\prime \prime } = \left( {M_1^2 -1} \right) \tan \theta \sin \theta +\cos \theta \\&{B}_1^{\prime \prime } = -2\sin \theta \\&\Gamma _1 :{E}_1^{\prime \prime } = \sin \theta \\&{A}_2^{\prime \prime } = \left( {M_2^2 -1} \right) \tan \left( {\theta -\delta } \right) \sin \left( {\theta -\delta } \right) +\cos \left( {\theta -\delta } \right) \\&{B}_2^{\prime \prime } = -2\sin \left( {\theta -\delta } \right) \\&\Gamma _2 :{E}_2^{\prime \prime } = \sin \left( {\theta -\delta } \right) \\&{C}^{\prime \prime } = \tan \left( {\theta -\delta } \right) -\tan \theta \\&{G}^{\prime \prime } = -{F}^{\prime \prime }{/}\cos \left( {\theta +\delta _1 } \right) \\&{F}^{\prime \prime } = \tan \left( {\theta -\delta } \right) \sin \left( {\theta -\delta } \right) \sin \delta _2 -\sin \theta \tan \theta \sin \delta _1 \end{aligned} \end{aligned}$$

(66)

Equation (65) can now be written as,

$$\begin{aligned} {L}^{\prime \prime }={A}_2^{\prime \prime } P_2 +{B}_2^{\prime \prime } D_2 +{E}_2^{\prime \prime } \Gamma _2 +{C}^{\prime \prime } S_a +{G}^{\prime \prime } S_b \end{aligned}$$

(67)

or,

$$\begin{aligned} L^{\prime \prime } =A_2^{\prime \prime } P_2 +B_2^{\prime \prime } D_2 +E_2^{\prime \prime } \Gamma _2 +C^{\prime \prime } S_a +F^{\prime \prime }/y \end{aligned}$$

(68)

where,

$$\begin{aligned} L^{\prime \prime }=A_1^{\prime \prime } P_1 +B_1^{\prime \prime } D_1 +E_1^{\prime \prime } \Gamma _1 \end{aligned}$$

(69)

Either one of the equations (67) or (68) can be used to solve for the post-shock vorticity, $\Gamma _2$, in terms of the other variables. The two equations differ in their last terms depending on whether the transverse curvature of the shock is specified by $S_b$ or y—a choice determined by the problem at hand. $S_b$ and y are themselves interchangeable through $S_b =-\cos \left( {\theta +\delta _1 } \right) {/}y$. Choosing (67) and solving (65) for $\Gamma _2$ gives the desired expression for the downstream vorticity,

(70)

This is the generalized vorticity equation in a rational form for ${\Gamma }_{2}$, the normalized vorticity behind a curved shock facing non-uniform, divergent flow. Together with equations (39), it forms three equations for the three unknowns $P_2, D_2$ and $\Gamma _2$ so as to completely define the non-uniform post-shock flow. For a uniform upstream, (70) reduces to,

$$\begin{aligned} \Gamma _2 =\left[ {\frac{{C}^{\prime \prime }}{{E}_2^{\prime \prime } }+\frac{\left[ {BC} \right] }{\left[ {AB} \right] }\frac{{A}_2^{\prime \prime } }{{E}_2^{\prime \prime }}-\frac{\left[ {AC} \right] }{\left[ {AB} \right] }\frac{{B}_2^{\prime \prime } }{{E}_2^{\prime \prime } }} \right] S_a \end{aligned}$$

(71)

The coefficient multiplying $S_{a}$ is identical to the coefficient of $S_{a}=\partial \theta /\partial \sigma$ in (55). Fortunately $P_2$ and $D_2$ are decoupled from $\Gamma _2$, leading to explicit solutions for all unknowns. $P_2$ and $D_2$, appearing in the equations (65) and (70), are found from the two curved shock equations (37) and (38) which are repeated here:

$$\begin{aligned} P_2&=\frac{B_2 \left( {C^{\prime } S_a +G^{\prime } S_b -L^{\prime }} \right) -B_2^{\prime } \left( {CS_a +GS_b -L} \right) }{A_2 B_2^{\prime } -A_2^{\prime } B_2 } \nonumber \\ D_2&=-\frac{A_2 \left( {C^{\prime } S_a +G^{\prime } S_b -L^{\prime }} \right) -A_2^{\prime } \left( {CS_a +GS_b -L} \right) }{A_2 B_2^{\prime } -A_2^{\prime } B_2 } \end{aligned}$$

(72)

where the L-terms above are given by,

$$\begin{aligned} L&=A_1 P_1 +B_1 D_1 +E_1 \Gamma _1 \nonumber \\ L^{\prime }&=A_1^{\prime } P_1 +B_1^{\prime } D_1 +E_1^{\prime } \Gamma _1 \end{aligned}$$

(73)

Note that L and $L^{\prime }$ contain the upstream gradients and that G and $G^{\prime }$ contain the upstream flow inclination $\delta _1$. Substituting $P_2$ and $D_2$ from (72) into (70) and collecting terms of the upstream gradients and the shock curvatures gives the influence coefficient form of the vorticity equation (70),

$$\begin{aligned} \Gamma _2 =I_p P_1 +I_d D_1 +I_g \Gamma _1 +I_a S_a +I_b S_b \end{aligned}$$

(74)

where the I-coefficients, each multiplying their respective variables, appear in the full equation for $\Gamma _2$ as shown below,

$$\begin{aligned} \Gamma _2= & {} \left\{ \left[ {AB} \right] A_1^{\prime \prime } +\left( {B_2 A_1^{\prime } -B_2^{\prime } A_1 } \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 A_1^{\prime } -A_2^{\prime } A_1 } \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} P_1 \nonumber \\&+\left\{ \left[ {AB} \right] B_1^{\prime \prime } +\left( {B_2 B_{1}^{\prime } -B_2^{\prime } B_1 } \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 B_1^{\prime } -A_2^{\prime } B_1 } \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime }} \right\} D_1 \nonumber \\&+\left\{ \left[ {AB} \right] E_1^{\prime \prime } +\left( {B_2 E_1^{\prime } -B_2^{\prime } E_1 } \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 E_1^{\prime } -A_2^{\prime } E_1 } \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} \Gamma _1 \nonumber \\&-\left\{ \left[ {AB} \right] C^{\prime \prime }+\left( {B_2 C^{\prime }-B_2^{\prime } C} \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 C^{\prime }-A_2^{\prime } C} \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} S_a \nonumber \\&-\left\{ \left[ {AB} \right] G^{\prime \prime }+\left( {B_2 G^{\prime }-B_2^{\prime } G} \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 G^{\prime }-A_2^{\prime } G} \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} S_b \end{aligned}$$

(75)

Fig. 6

Influence coefficients for vorticity behind the shock as by (74)

Fig. 7

Plot of the $I_{\mathrm{b}}$ influence coefficient against shock angle with the pre-shock flow divergence angle as parameter

The unprimed and single-primed coefficients, $A\ldots G$, are listed as equations (34, 35); the double-primed are in (66). Equation (75) shows clearly what the role is of each upstream non-uniformity $P_1, D_1$ and $\Gamma _1$ and of the shock curvatures $S_a$ and $S_b$ in determining the downstream vorticity, $\Gamma _2$. Note that the above derivation for vorticity does not need Crocco’s thermodynamic relation between vorticity and entropy gradient, and that the resulting equations account for upstream flow non-uniformity and vorticity as well as flow divergence. Derivation of the vorticity equation parallels those for the pressure gradient and streamline curvature but it is quite a bit simpler. The use of j to denote planar or axial symmetry has been dropped since the equations are uniformly valid for both geometries. For axial flow, y is the radius of the shock’s curvature in the transverse plane, so that the flow is sensitive to dimensionality through the parameter y. In the calculations for planar flow, y is set to a very large number. Figure 6 depicts the influence coefficients for vorticity plotted against shock angle. The blue curve shows the influence of pre-shock pressure gradient $P_1$, and we see that a positive pressure gradient causes a positive vorticity contribution for an acute shock and a negative contribution for an obtuse shock. The green curve shows that a positive pre-shock flow curvature, $D_1$ produces a positive contribution to vorticity. The red curve is for the effect of pre-shock vorticity itself. At the Mach wave limits, the influence coefficient has a value of 1, predicting that vorticity passes through Mach waves unchanged. All other curves are at zero so, at Mach wave conditions, there is no vorticity production due to pre-shock gradients or Mach wave curvatures. Stronger shocks tend to amplify and reverse the direction of vorticity. The cyan curve shows that positive vorticity is produced by a positive flow-plane shock curvature, $S_a$, for an acute shock and negative vorticity is produced by a positively curving obtuse shock. The black curve is for the effect of the transverse shock curvature, $S_b$, and it shows that the influence coefficient for the transverse curvature is identically zero. This confirms the fact that the shock produces vorticity only by its flow-plane curvature and not by the transverse curvature so that flow behind a conical shock is irrotational. For flows with no pre-shock divergence/convergence, the $I_b S_b$ term can be dropped from equations (74) and (75) since $I_{b}$ is identically zero.

The situation becomes complicated when the pre-shock flow is diverging. The role played by flow divergence $\delta _1$ and transverse shock curvature $S_b$ is interactive and has to be carefully considered. From what we know of the behaviour of vorticity, it seems incorrect that post-shock vorticity is a function of the cross-stream curvature, $S_b$, as evident from the last term of (75). So we examine the influence coefficient for $S_b$,

$$\begin{aligned} \hbox { I}_b= & {} -\left\{ \left[ {AB} \right] G^{\prime \prime }+\left( {B_2 G^{\prime }-B_2^{\prime } G} \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 G^{\prime }-A_2^{\prime } G} \right) B_2^{\prime \prime } \right\} /\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} \end{aligned}$$

(76)

In particular its numerator,

$$\begin{aligned} \hbox { N}_b = \left[ {AB} \right] G^{\prime \prime }+\left( {B_2 G^{\prime }-B_2^{\prime } G} \right) A_2^{\prime \prime } -\left( {A_2 G^{\prime }-A_2^{\prime } G} \right) B_2^{\prime \prime }\nonumber \\ \end{aligned}$$

(77)

must be zero when $\delta _1$ is zero. The black curve in Fig. 6 shows that it is indeed so. Note that $\delta _1$ is contained in $G^{\prime }$ and $G^{\prime \prime }$ only and not in G. This requires that the part of $\hbox {N}_{b}$, not containing $\delta _1$ equals zero, i.e.,

$$\begin{aligned} A_{2}^{{\prime }} B_{2}^{{\prime \prime }} -B_{2}^{{\prime }} A_{2}^{{\prime \prime }} =0 \end{aligned}$$

(78)

This has proven that there is no influence on post-shock vorticity from $S_b$ when there is no pre-shock divergence. The proof of this is straightforward, with four lines of algebra, so that, without loss of generality, the influence coefficient for $S_{b}$ can be simplified to,

$$\begin{aligned} I_b = -\left\{ {\left[ {AB} \right] G^{\prime \prime }+\left( {B_2 G^{\prime }} \right) A_2^{\prime \prime } -\left( {A_2 G^{\prime }} \right) B_2^{\prime \prime } } \right\} /\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} \nonumber \\ \end{aligned}$$

(79)

$I_{b}$ from this equation is plotted in Fig. 7, against the shock angle, for Mach 3, with the divergence angle $\delta _1$ ($^\circ$) as parameter. Actually it is $I_{\mathrm{b}}\times S_{\mathrm{b}}\times y$ because $I_{\mathrm{b}}$ by itself goes to infinity when $\cos \left( {\theta +\delta _1 } \right)$ goes to zero and it gets hard to display. Note that $\cos \left( {\theta +\delta _1 } \right) = -S_{b}\times y$. The green line is for $\delta _1 = 0$, black curves are for positive $\delta _1$ increasing by 10$^\circ$ away from the zero line to 50. Red curves are for negative $\delta _1$ decreasing by 10$^\circ$ to −50$^\circ$.